��Ŀ����
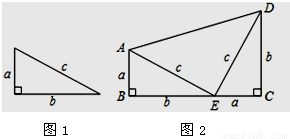
���ɶ�����һ�����ϵ���ѧ���������кܶ���֤���������ҹ�������ѧ����ˬ������ͼ���������������֤����������ѧ�һ�������ѡ����ι�ϵ�������ɶ�������������������Ϊ�����������������ˡ����е�һ�Ρ�̸���������ԣ������ͼ1��ֱ���������������ɶ�����
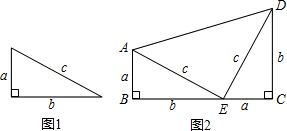
��ͼ1�е�ֱ��������Ϊ���������Թ������a��bΪ�ף���a+bΪ�ߵ�ֱ�����Σ���ͼ2������������ͼ2����֤���ɶ�����
����ͼ2�е�ֱ�����Σ����ǿ���֤��
| a+b |
| c |
| 2 |
��BC=a+b��AD=
�֡���ֱ������ABCD����BC
��
| a+b |
| c |
| 2 |
����������SAS��֤��ABE�ա�ECD���ɵö�Ӧ����ȣ����90��Ľǣ���֤��AED=90�㣬�������������������ֱ�������ε�����ͣ���֤a2+b2=c2����ֱ������ABCD�У�BC��AD��������֤��AED��ֱ�������Σ���ô���ù��ɶ�����AD=
c���Ӷ���֤
��
��
| 2 |
| a+b |
| c |
| 2 |
����⣺���ֱ�������ε���ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����ôa2+b2=c2��
��Rt��ABE��Rt��ECD��
���AEB=��EDC��
�֡ߡ�EDC+��DEC=90�㣬
���AEB+��DEC=90�㣻
���AED=90�㣻��5�֣�
S����ABCD=SRt��ABE+SRt��DEC+SRt��AED
��a+b����a+b��=
ab+
ab+
c2��
��a2+2ab+b2��=
ab+
ab+
c2��
������a2+b2=c2��7�֣���
AD=
c��BC��AD��a+b��
c����10�֣�
��Rt��ABE��Rt��ECD��
���AEB=��EDC��
�֡ߡ�EDC+��DEC=90�㣬
���AEB+��DEC=90�㣻
���AED=90�㣻��5�֣�
S����ABCD=SRt��ABE+SRt��DEC+SRt��AED
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
������a2+b2=c2��7�֣���
AD=
| 2 |
| 2 |
����������������ȫ�������ε��ж������ʡ�����ָ�����ɶ�����֪ʶ��

��ϰ��ϵ�д�
�����Ŀ

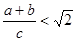 ����֤���������£�
����֤���������£�