题目内容
勾股定理是一条古老的数学定理,它有很多种证明方法.
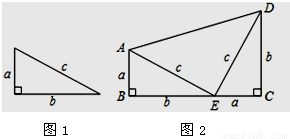
(1)请你根据图1填空;勾股定理成立的条件是
(2)以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
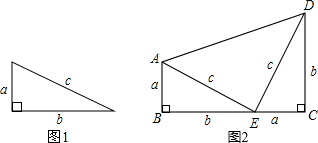
(1)请你根据图1填空;勾股定理成立的条件是
直角
直角
三角形,结论是a2+b2=c2
a2+b2=c2
(三边关系)(2)以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;

分析:(1)根据图示直接填空;
(2)利用S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED进行解答.
(2)利用S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED进行解答.
解答:解:(1)勾股定理指的是在直角三角形中,两直角边的平方的和等于斜边的平方.
故答案是:直角;a2+b2=c2;
(2)∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴
(a+b)(a+b)=
ab+
ab+
c2.
整理,得a2+b2=c2.
故答案是:直角;a2+b2=c2;
(2)∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理,得a2+b2=c2.
点评:本题考查了勾股定理的证明.解答该题时,利用了“数形结合”的数学思想.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
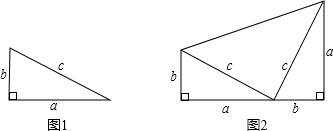
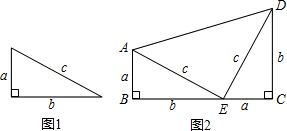

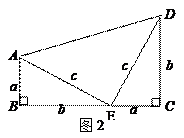
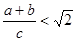 ,其证明步骤如下:
,其证明步骤如下: