题目内容
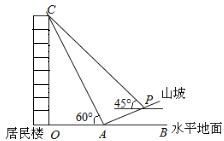
【题目】如图 ,一幢居民楼OC临近山坡AP,山坡AP的坡度为i=1:![]() ,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,
,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,![]() ≈1.73)
≈1.73)
【答案】32
【解析】分析:作PE⊥OB于点E,PF⊥CO于点F,如图,设PE=x,则AE=![]() x,在Rt△AEP中根据勾股定理可得PE=5,则AE=
x,在Rt△AEP中根据勾股定理可得PE=5,则AE=![]() ;设CF=PF=m米,则OC=(m+5)米、OA=(m- -
;设CF=PF=m米,则OC=(m+5)米、OA=(m- -![]() )米,在Rt△AOC中,由tan60°=
)米,在Rt△AOC中,由tan60°=![]() 求得m的值,继而可得答案.
求得m的值,继而可得答案.
详解:过点P作PE⊥OB交OB于点E,PF⊥OC交OC于点F,
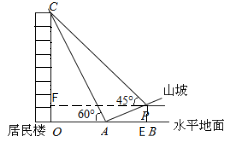
∵i=1:![]() , AP=10
, AP=10
设PE=x,则AE=![]() x,
x,
在Rt△AEP中,x2+(![]() x)2=102,
x)2=102,
解得:x=5或x=-5(舍),
∴PE=5,则AE=![]() ,
,
∵∠CPF=∠PCF=45°,
∴CF=PF,
设CF=PF=m米,则OC=(m+5)米,OA=(m-![]() )米,
)米,
在Rt△AOC中,![]() ,即
,即![]() ,
,
解得:m=10(![]() +1),
+1),
∴OC=10(![]() +1)+5≈32米,
+1)+5≈32米,
答:塑像的高度约为32米.

【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个) 的变化如下表:同时,销售过程中的其他开支(不含进价)总计40万元.
销售价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的数据,用所学过的函数知识,直接写出y与 x的函数解析式;
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格 x(元/个) 的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请你结合函数图象求出销售价格 x(元/个) 的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元 ?