题目内容
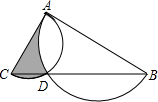 如图,以直角三角形的两条直角边AC、AB为直径,向三角形内作半圆,两半圆交于点D,CD=1,BD=3,则图中阴影部分的面积为
如图,以直角三角形的两条直角边AC、AB为直径,向三角形内作半圆,两半圆交于点D,CD=1,BD=3,则图中阴影部分的面积为分析:连接AD,则AD⊥BC,则△ACD∽△BCA;根据相似三角形的对应边的比相等,可以求出AC=2,因而∠B=30度,根据扇形的面积公式就可以求出两个半圆的公共部分的面积.用以AC为直径的半圆的面积,减去公共部分的面积就得到阴影部分的面积.
解答: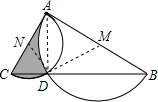 解:如图,设N是以AC为直径的半圆的圆心,连接ND,M为以AB为直径的半圆的圆心,连接MD,连接AD.
解:如图,设N是以AC为直径的半圆的圆心,连接ND,M为以AB为直径的半圆的圆心,连接MD,连接AD.
则AD⊥BC,根据射影定理有:
AC2=CD•CB=CD(CD+BD)=4,即AC=2;
同理可求得AB=2
;
因此∠ABD=30°,∠ACD=60°;
∴∠AMD=60°,∠AND=120°.
∴扇形MAD中,弓形AD的面积=S扇形MAD-S△MAD=
-
=
-
;
同理可求得扇形AND中,S弓形AD=
-
;
因此S阴影=
-(
-
+
-
)=
-
(平方单位).
 解:如图,设N是以AC为直径的半圆的圆心,连接ND,M为以AB为直径的半圆的圆心,连接MD,连接AD.
解:如图,设N是以AC为直径的半圆的圆心,连接ND,M为以AB为直径的半圆的圆心,连接MD,连接AD.则AD⊥BC,根据射影定理有:
AC2=CD•CB=CD(CD+BD)=4,即AC=2;
同理可求得AB=2
| 3 |
因此∠ABD=30°,∠ACD=60°;
∴∠AMD=60°,∠AND=120°.
∴扇形MAD中,弓形AD的面积=S扇形MAD-S△MAD=
60×π×(
| ||
| 360 |
3
| ||
| 4 |
| π |
| 2 |
3
| ||
| 4 |
同理可求得扇形AND中,S弓形AD=
| π |
| 3 |
| ||
| 4 |
因此S阴影=
| π |
| 2 |
| π |
| 2 |
3
| ||
| 4 |
| π |
| 3 |
| ||
| 4 |
| 3 |
| π |
| 3 |
点评:不规则的图形的面积一般要转化为一些规则图形的面积的和或差来求解.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
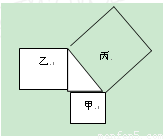
 7、如图,以直角三角形的三边为边向三角形外作正方形,已知甲、乙两个正方形的面积分别为4、6,则丙正方形的面积为
7、如图,以直角三角形的三边为边向三角形外作正方形,已知甲、乙两个正方形的面积分别为4、6,则丙正方形的面积为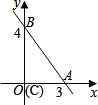 如图,以直角三角形的直角顶点C为原点,以CA所在的直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为
如图,以直角三角形的直角顶点C为原点,以CA所在的直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为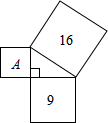 如图,以直角三角形的三边为边长分别作三个正方形,其中两个正方形的面积标示在图中,则字母A所在的正方形的面积是
如图,以直角三角形的三边为边长分别作三个正方形,其中两个正方形的面积标示在图中,则字母A所在的正方形的面积是