题目内容
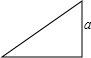如图，一个直角三角形的三边长均为正整数，已知它的一条直角边的长恰是3，那么另一条直角边的长是分析：根据勾股定理，两边的平方和等于第三边的平方，设另一条直角边a，根据勾股定理可以得出斜边为
，根据边长的关系，两边之和大于第三边，两边之差小于第三边，结合边长为整数，进而得出a的值．
| 9+a2 |
解答：解：设另一个直角边为a，
则根据勾股定理可以得出斜边为
，
由三角形的边长关系：
3+a＞
，
∵边长为整数，
∴a=4，
即斜边为5．
即另一条直角边的长是4．
则根据勾股定理可以得出斜边为
| 9+a2 |
由三角形的边长关系：
3+a＞
| 9+a2 |
∵边长为整数，
∴a=4，
即斜边为5．
即另一条直角边的长是4．
点评：本题考查了勾股定理的应用，属于比较简单的题目，需要熟练掌握．
练习册系列答案
相关题目
如图，一个直角三角形纸板，其两条直角边长分别为6cm和8cm，小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体．请你帮小明推算出这个旋转体的全面积．（π取3.14）
如图，一个直角三角形的三边长均为正整数，已知它的一条直角边的长恰是1997，那么另一条直角边的长为
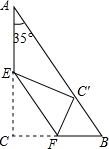如图是一个直角三角形的纸片，将直角沿EF折叠，使C点落在AB边上，并且使∠EC′A=∠A，那么∠C′FE的度数是（ ）| A、50° | B、45° | C、55° | D、70°第7题图 |