题目内容
(2011四川泸州,16,3分)已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,则k的值为 .
k=1
由题意设方程x2+(2k+1)x+k2-2=0两根为x1,x2,得x1+x2=-(2k+1),x1?x2=k2-2,然后再根据两实根的平方和等于11,从而解出k值.
解:设方程x2+(2k+1)x+k2-2=0两根为x1,x2
得x1+x2=-(2k+1),x1?x2=k2-2,
△=(2k+1)2-4×(k2-2)=4k+9>0,
∴k>-9/4,
∵x12+x22=11,
∴(x1+x2)2-2x1x2=11,
∴(2k+1)2-2(k2-2)=11,
解得k=1或-3;
∵k>-9/4,
故答案为k=1.
解:设方程x2+(2k+1)x+k2-2=0两根为x1,x2
得x1+x2=-(2k+1),x1?x2=k2-2,
△=(2k+1)2-4×(k2-2)=4k+9>0,
∴k>-9/4,
∵x12+x22=11,
∴(x1+x2)2-2x1x2=11,
∴(2k+1)2-2(k2-2)=11,
解得k=1或-3;
∵k>-9/4,
故答案为k=1.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
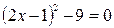 (2)
(2)
 )解方程:
)解方程: .
.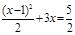 化为一元二次方程的一般形式是________ ,它的一次项系
化为一元二次方程的一般形式是________ ,它的一次项系 的解是 ▲ .
的解是 ▲ .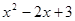 =0的根的情况是
=0的根的情况是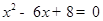 的两个根,则这个三角形的周
的两个根,则这个三角形的周
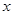 的方程
的方程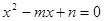 的两个根是0和
的两个根是0和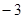 ,则
,则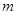 = ,
= , = .
= .