Question

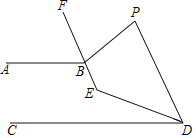
【题目】如图已知AB∥CD，P为直线AB，CD外一点，BF平分∠ABP，DE平分∠CDP，BF的反向延长线交DE于点E．

（1）∠ABP，∠P和∠PDC的数量关系为　 　；

（2）若∠BPD＝80°，求∠BED的度数；

（3）∠P与∠E的数量关系为　 　．

Answer 1

【答案】（1）∠ABP＝∠P+∠ADC；（2）∠BED＝140°；（3）∠BED+P＝180°．

【解析】

（1）延长AB交PD于G，根据平行线的性质得到∠PGA＝∠PDC，根据三角形的外角的性质即可得到结论；

（2）延长FE交CD于H，根据平行线的性质和角平分线的定义即可得到结论；

（3）根据平行线的性质和角平分线的定义即可得到结论．

解：（1）延长AB交PD于G，

∵AG∥CD，

∴∠PGA＝∠PDC，

∵∠ABP＝∠P+∠AGP，

∴∠ABP＝∠P+∠ADC，

故答案为：∠ABP＝∠P+∠ADC；

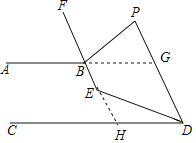
（2）延长FE交CD于H，

∵AB∥CD，

∴∠ABF＝∠CHB，

∵BF平分∠ABP，DE平分∠CDP，

∴∠ABF＝∠CHB＝ABP，∠HDE＝PDC，

∵∠ABP＝∠P+∠ADC，

∴∠CHE＝（∠P+∠PDC）＝40°+∠HDE，

∵∠CHE＝∠HDE+∠DEH，

∴∠DEH＝40°，

∴∠BED＝180°﹣∠DEH＝140°；

（3）由（2）知，∠CHE＝（∠P+∠PDC）＝P+∠HDE，

∵∠CHE＝∠DEH+∠HDE，

∴∠DEH＝∠P，

∴∠BED＝180°﹣∠P．

∴∠BED+P＝180°．

故答案为：∠BED+P＝180°．