题目内容
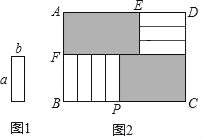
【题目】现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )

A. a=2bB. a=3bC. a=3.5bD. a=4b
【答案】B
【解析】
表示出左上角与右下角部分的面积,求出之差,根据差与BC无关即可求出a与b的关系式.
解:法1:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AEAF﹣PCCG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
法2:既然BC是变化的,当点P与点C重合开始,然后BC向右伸展,
设向右伸展长度为x,左上阴影增加的是3bx,右下阴影增加的是ax,因为S不变,
∴增加的面积相等,
∴3bx=ax,
∴a=3b.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】学校开展校外宣传活动,有社区板报(A)、集会演讲(B)、喇叭广播(C)、发宣传画(D)四种方式.围绕“你最喜欢的宣传方式”,校团委在全校学生中进行了抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下不完整的统计图表.
选项 | 方式 | 百分比 |
A | 社区板报 | m |
B | 集会演讲 | 30% |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共 人,m= ;
(2)若该校学生有900人,估计其中喜欢“集会演讲”宣传方式的学生约有多少人?