题目内容
(2012•长春一模)如图,梯形OABC中,OA在x轴上,CB∥OA,∠OAB=90°,O为坐标原点,B(4,4),BC=2,动点Q从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作QP⊥x轴交折线O-C -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
(1)求tan∠AOC;
(2)求S与t的函数关系式;
(3)求(2)中的S的最大值;
(4)连接AC,AC的中点为M,请直接写出在正方形PQRS变化过程中,t为何值时,△PMS为等腰三角形.
 -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)(1)求tan∠AOC;
(2)求S与t的函数关系式;
(3)求(2)中的S的最大值;
(4)连接AC,AC的中点为M,请直接写出在正方形PQRS变化过程中,t为何值时,△PMS为等腰三角形.
分析:(1)过C作CD⊥x轴于D,由B的坐标得出AB的长,再由C的坐标得出OD的长,根据四边形ABCD为矩形,得到对边相等,即CD=AB,在直角三角形OCD中,利用锐角三角函数定义表示出tan∠AOC;
(2)根据Q的位置分三种情况考虑:当0≤x≤
时;当
≤x≤2时;当2≤x≤4时;讨论求得S与t的函数关系式;
(3)由(2)得出的S与t的关系式,利用一次函数及二次函数的性质求出三个函数的最大值,比较后即可求出S的最大值;
(4)分三种情况考虑:PS=MS;MP=MS;PS=PM,列出方程即可得到t的值.
(2)根据Q的位置分三种情况考虑:当0≤x≤
| 4 |
| 3 |
| 4 |
| 3 |
(3)由(2)得出的S与t的关系式,利用一次函数及二次函数的性质求出三个函数的最大值,比较后即可求出S的最大值;
(4)分三种情况考虑:PS=MS;MP=MS;PS=PM,列出方程即可得到t的值.
解答:解:(1)过C作CD⊥x轴于D,则OD=2,CD=4,
则tan∠AOC=2;
(2)当运动到R与A重合时,此时OQ=t,AQ=PQ=4-t
则tan∠AOC=
=
=2,
解得t=
.
当0≤x≤
时,S=PQ2=(2OQ)2=(2t)2=4t2;
当
≤x≤2时,S=PQ•AQ=2t•(4-t)=-2t2+8t;
当2≤x≤4时,S=4 AQ=4(4-t)=-4t+16;
(3)当0≤x≤
时,t=
时,t最大=
;
当
≤x≤2时,t=2,t最大=8;
当2≤x≤4时,t=2,t最大=8;
综上,t=2时S最大=8.
(4)当t1=
,t2=
,t3=2
-1时,△PMS为等腰三角形.
则tan∠AOC=2;
(2)当运动到R与A重合时,此时OQ=t,AQ=PQ=4-t
则tan∠AOC=
| PQ |
| OQ |
| 4-t |
| t |
解得t=
| 4 |
| 3 |
当0≤x≤
| 4 |
| 3 |
当
| 4 |
| 3 |
当2≤x≤4时,S=4 AQ=4(4-t)=-4t+16;
(3)当0≤x≤
| 4 |
| 3 |
| 4 |
| 3 |
| 64 |
| 9 |
当
| 4 |
| 3 |
当2≤x≤4时,t=2,t最大=8;
综上,t=2时S最大=8.
(4)当t1=
13-2
| ||
| 9 |
| 3 |
| 2 |
| 3 |
点评:此题考查了相似形综合题,涉及的知识有:坐标与图形性质,锐角三角函数定义,正方形的性质,以及一次函数与二次函数的性质,利用了数形结合及分类讨论的数学思想,是一道较难的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
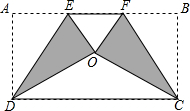 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x-