题目内容
已知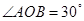 ,点
,点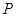 在
在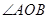 内部,
内部,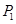 与
与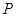 关于
关于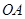 对称,
对称,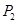 与
与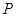 于
于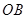 对称,则
对称,则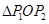 的形状一定是()
的形状一定是()
直角三角形 (B)等边三角形
(C)底边和腰不相等的等腰三角形 (D)钝角三角形
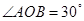 ,点
,点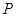 在
在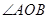 内部,
内部,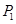 与
与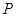 关于
关于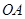 对称,
对称,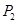 与
与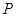 于
于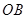 对称,则
对称,则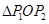 的形状一定是()
的形状一定是()直角三角形 (B)等边三角形
(C)底边和腰不相等的等腰三角形 (D)钝角三角形
B
根据轴对称的性质,结合等边三角形的判定求解.
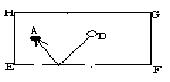
 解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°,
∴△OP1P2是等边三角形.
故选:B.
此题考查了轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
 解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°,
∴△OP1P2是等边三角形.
故选:B.
此题考查了轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目




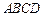 中,点F在边BC上,E在边BA的延长线上.
中,点F在边BC上,E在边BA的延长线上.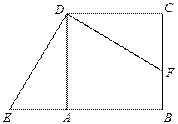
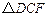 按顺时针方向旋转后恰好与
按顺时针方向旋转后恰好与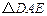 重合.则旋转
重合.则旋转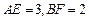 ,求四边形
,求四边形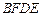 的面积.
的面积.