Question

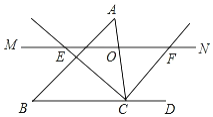
【题目】如图，在△ABC与△A'B'C'中，∠A＝∠A'，BD、CE是△ABC的高，B'D'、C'E'是△A'B'C'的高，点D、E、D'、E'分别在AC、AB、A'C'、A'B'上，且．

求证：

Answer 1

【答案】见解析.

【解析】

先证△BDC∽△B′D′C′得∠ACB=∠A′C′B′，结合∠A=∠A′可证△ABC∽△A'B'C'，再利用相似三角形的性质可得答案．

∵BD是AC边上的高、B'D'是A'C'的高，

∴∠BDC=∠B′D′C′=90°，

∴△BDC和△B′D′C′均为直角三角形，

∵，

∴△BDC∽△B′D′C′，

∴∠ACB=∠A′C′B′，

∵∠A=∠A′，

∴△ABC∽△A'B'C'，

∵BD、CE是△ABC的高，B'D'、C'E'是△A'B'C'的高，

∴．