题目内容
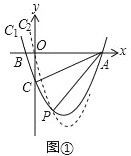
【题目】如图①,在平面直角坐标系中,抛物线C1:y=(x+k)(x﹣3)交x轴于点A、B(A在B的右侧),交y轴于点C,横坐标为2k的点P在抛物线C1上,连结PA、PC、AC,设△ACP的面积为S.
(1)求直线AC对应的函数表达式(用含k的式子表示).
(2)当点P在直线AC的下方时,求S取得最大值时抛物线C1所对应的函数表达式.
(3)当k取不同的值时,直线AC、抛物线C1和点P、点B都随k的变化而变化,但点P始终在不变的抛物线(虚线)C2:y=ax2+bx上,求抛物线C2所对应的函数表达式.
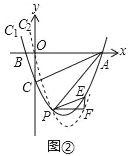
(4)如图②,当点P在直线AC的下方时,过点P作x轴的平行线交C2于点F,过点F作y轴的平行线交C1于点E,当△PEF与△ACO的相似比为![]() 时,直接写出k的值.
时,直接写出k的值.
【答案】(1)y=kx﹣3k;(2)C1:y=x2﹣![]() ﹣
﹣![]() ;(3)C2:y=
;(3)C2:y=![]() x2﹣
x2﹣![]() x;(4)k的值为
x;(4)k的值为![]() 或
或![]() .
.
【解析】分析:(1)先求点A和C的坐标,利用待定系数法求直线AC的解析式;
(2)如图①,作辅助线,构建铅直线PM,利用S△PAC=S△PQC+S△PQA表示S的关系式,设![]() 表示PQ的长,代入可得S与k的关系式,利用顶点式求最值,将k值代入C1的解析式即可;
表示PQ的长,代入可得S与k的关系式,利用顶点式求最值,将k值代入C1的解析式即可;
(3)任意取两个k的值代入到点P的坐标中,如:当k=1时,此时P(2,3),当k=2时,P(4,6),代入抛物线C2所对应的函数表达式中可得结论;
(4)如图②,由△ACO和△PEF都是直角三角形,相似比为![]() ,所以存在两种情况:
,所以存在两种情况:
①当△PEF∽△CAO时,![]() ②当
②当![]() 时,
时,![]() 列比例式,根据点P的纵坐标的绝对值等于点E的纵坐标的绝对值与EF的和列等式可得k的值,并根据题意进行取舍.
列比例式,根据点P的纵坐标的绝对值等于点E的纵坐标的绝对值与EF的和列等式可得k的值,并根据题意进行取舍.
详解:(1)在y=(x+k)(x3)中,
令y=0,可得A(3,0),B(k,0),
令x=0,可得C(0,3k),
设直线AC对应的函数表达式为:y=mx+n,
将A(3,0),C(0,3k)代入得:![]()
解得:![]()
∴直线AC对应的函数表达式为:y=kx3k;
(2)如图①,过点P作y轴的平行线交AC于点Q,交x轴于点M,
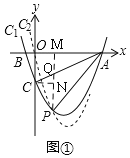
过C作CN⊥PM于N,
当x=2k时,![]()
∵点P、Q分别在抛物线C1、直线AC上,
∴![]()
∴![]()
∴S△PAC=S△PQC+S△PQA![]()
![]()
∴当![]() 时,△PAC面积的最大值是
时,△PAC面积的最大值是![]()
此时,C1:![]()
(3)∵点P在抛物线C1上,
∴P(2k,6k29k),
当k=1时,此时P(2,3),当k=2时,P(4,6),
把(2,3)和(4,6)代入抛物线(虚线)C2:![]() 上得:
上得:
![]() 解得:
解得: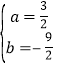 ,
,
∴抛物线C2所对应的函数表达式为:![]()
(4)如图②,由题意得:△ACO和△PEF都是直角三角形,且![]() ,
,
∵点P在直线AC的下方,横坐标为2k的点P在抛物线C1上,
∴P(2k,6k29k),且![]() ,
,
∵A(3,0),C(0,3k),
∴OA=3,OC=3k,
∴当△PEF与△ACO的相似比为![]() 时,存在两种情况:
时,存在两种情况:
①当△PEF∽△CAO时,![]()
∴![]()
∴PF=k,EF=1,
∴![]()
∵EF=1,
∴![]()
![]()
![]() (舍),
(舍),
②当△PEF∽△ACO时, ![]()
∴![]()
∴PF=1,EF=k,
∴![]()
∴![]()
![]()
综上所述,k的值为![]() 或
或![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案