Question

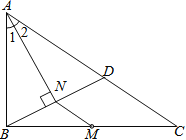
【题目】如图，已知AD为△ABC的高，AD＝BC，以AB为底边作等腰Rt△ABE，EF∥AD，交AC于F，连ED，EC，有以下结论：①△ADE≌△BCE；②CE⊥AB；③BD＝2EF；④S△BDE＝S△ACE，其中正确的是（　　）

A.①②③B.②④C.①③D.①③④

Answer 1

【答案】D

【解析】

①易证∠CBE=∠DAE，即可求证：△ADE≌△BCE；
②根据①结论可得∠AEC=∠DEB，即可求得∠AED=∠BEG，即可解题；
③证明△AEF≌△BED即可；
④易证△FDC是等腰直角三角形，则CE=EF，S△AEF=S△ACE，由△AEF≌△BED，可知S△BDE=S△ACE，所以S△BDE=S△ACE．

如图延长CE交AD于K，交AB于H．设AD交BE于O．

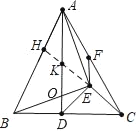
∵∠ODB＝∠OEA，∠AOE＝∠DOB，

∴∠OAE＝∠OBD，

∵AE＝BE，AD＝BC，

∴△ADE≌△BCE，故①正确，

∴∠AED＝∠BEC，DE＝EC，

∴∠AEB＝∠DEC＝90°，

∴∠ECD＝∠ABE＝45°，

∵∠AHC＝∠ABC+∠HCB＝90°+∠EBC＞90°，

∴EC不垂直AB，故②错误，

∵∠AEB＝∠HED，

∴∠AEK＝∠BED，

∵AE＝BE，∠KAE＝∠EBD，

∴△KAE≌△DBE，

∴BD＝AK，

∵△DCK是等腰直角三角形，DE平分∠CDK，

∴EC＝EK，

∵EF∥AK，

∴AF＝FC，

∴AK＝2EF，

∴BD＝2EF，故③正确，

∵EK＝EC，

∴S△AKE＝S△AEC，

∵△KAE△DBE，

∴S△KAE＝S△BDE，

∴S△BDE＝S△AEC，故④正确．

故选：D．