Question

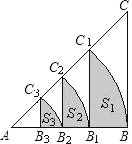
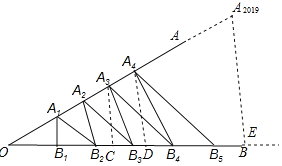
【题目】如图，∠AOB为锐角，在射线OA上依次截取A1A2＝A2A3＝A3A4＝…＝AnAn+1，在射线OB上依次截取B1B2＝B2B3＝B3B4＝…＝BnBn+1，记Sn为△AnBnBn+1的面积（n为正整数），若S3＝7，S4＝10，则S2019＝（　　）

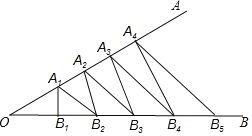
A.4039B.4041C.6055D.6058

Answer 1

【答案】C

【解析】

过A3作A3C⊥OB于C，过A4作A4D⊥OB于D，过A2019作A2019E⊥OB于E，则△OA3C∽△OA4D∽△OA2019E，设OA1＝a，A1A2＝A2A3＝A3A4＝…＝AnAn+1＝1个单位，由等底的三角形面积比等于三角形的高之比，得出，即，可得a＝，由相似三角形的性质得出，即可求出S2019＝6055．

解：过A3作A3C⊥OB于C，过A4作A4D⊥OB于D，过A2019作A2019E⊥OB于E，

则△OA3C∽△OA4D∽△OA2019E，

设OA1＝a，A1A2＝A2A3＝A3A4＝…＝AnAn+1＝1个单位，

∵S3＝7，S4＝10，B1B2＝B2B3＝B3B4＝…＝BnBn+1，

∴，

即，

解得：a＝，

∴，

∴，

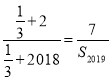∴S2019＝6055，

故选：C．