题目内容
如图,点A、B的坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,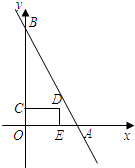 四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.
四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,求t的值;
(2)当t=4时,求S的值;
(3)直接写出S与t的函数关系式(不必写出解题过程);
(4)若S=12,则t=
分析:(1)证明△BCD∽△BOA,利用线段比求出t值.
(2)当t=4时,点E与A重合,证明△CBF∽△OBA求出CF.
(3)根据t的取值范围求出S的值.
(2)当t=4时,点E与A重合,证明△CBF∽△OBA求出CF.
(3)根据t的取值范围求出S的值.
解答:解:(1)由题意可得∠BCD=∠BOA=90°,∠CBD=∠OBA,
∴△BCD∽△BOA,
∴
=
而CD=OE=t,BC=8-CO=8-
,OA=4,
则
=
,
解得t=
,
∴当点D在直线AB上时,t=
.(2分)
(2)当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得
=
,
即
=
,
解得CF=3,
∴S=
OC(OE+CF)=
×2×(3+4)=7.(3分)
(3)①当0<t≤
时,S=
t2(1分)
②当
<t≤4时,S=-
t2+10t-16(1分)
③当4<t≤16时,S=-
t2+2t(1分)
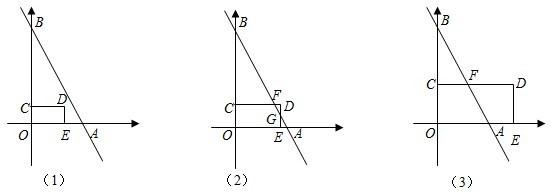
分析:①当0<t≤
时,如图(1),
②当
<t≤4时,如图(2),
∵A(4,0),B(0,8),∴直线AB的解析式为y=-2x+8,
∴G(t,-2t+8),F(4-
,
),
∴DF=
t-4,DG=
t-8,
∴S=S矩形COED-S△DFG=t•
-
(
t-4)(
t-8)=-
t2+10t-16
③当4<t≤16时,如图(3)
∵CD∥OA,∴△BCF∽△BOA,∴
=
,∴
=
,∴CF=4-
,
∴S=S△BOA-S△BCF=
×4×8-
×(4-
)(8-
)=-
t2+2t
(4)8(2分)
分析:由题意可知把S=12代入S=-
t2+2t中,-
t2+2t=12,
整理,得t2-32t+192=0,
解得t1=8,t2=24>16(舍去),
∴当S=12时,t=8.
∴△BCD∽△BOA,
∴
| BC |
| BO |
| CD |
| OA |
而CD=OE=t,BC=8-CO=8-
| t |
| 2 |
则
8-
| ||
| 8 |
| t |
| 4 |
解得t=
| 16 |
| 5 |
∴当点D在直线AB上时,t=
| 16 |
| 5 |
(2)当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得
| CF |
| CB |
| OA |
| OB |
即
| CF |
| 8-2 |
| 4 |
| 8 |
解得CF=3,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)①当0<t≤
| 16 |
| 5 |
| 1 |
| 2 |
②当
| 16 |
| 5 |
| 17 |
| 16 |
③当4<t≤16时,S=-
| 1 |
| 16 |
分析:①当0<t≤
| 16 |
| 5 |
②当
| 16 |
| 5 |
∵A(4,0),B(0,8),∴直线AB的解析式为y=-2x+8,
∴G(t,-2t+8),F(4-
| t |
| 4 |
| t |
| 2 |
∴DF=
| 5 |
| 4 |
| 5 |
| 2 |
∴S=S矩形COED-S△DFG=t•
| t |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 17 |
| 16 |
③当4<t≤16时,如图(3)
∵CD∥OA,∴△BCF∽△BOA,∴
| BC |
| BO |
| CF |
| OA |
8-
| ||
| 8 |
| CF |
| 4 |
| t |
| 4 |
∴S=S△BOA-S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 4 |
| t |
| 2 |
| 1 |
| 16 |
(4)8(2分)
分析:由题意可知把S=12代入S=-
| 1 |
| 16 |
| 1 |
| 16 |
整理,得t2-32t+192=0,
解得t1=8,t2=24>16(舍去),
∴当S=12时,t=8.

点评:本题考查的是二次函数的综合运用,相似三角形的判定以及考生的做题能力.

练习册系列答案
相关题目
 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为 15、如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为
15、如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为
 △OA′B′的位置
△OA′B′的位置 (2013•德惠市一模)如图,点A、B的坐标分别为(1,0)、(0,1),点P是第一象限内直线y=-x+3上的一个动点,当点P的横坐标逐渐增大时,四边形OAPB的面积( )
(2013•德惠市一模)如图,点A、B的坐标分别为(1,0)、(0,1),点P是第一象限内直线y=-x+3上的一个动点,当点P的横坐标逐渐增大时,四边形OAPB的面积( ) 如图,点O、B的坐标分别为(0,0)(3,0),将△OAB绕O点按逆时针方向旋转90°得到△OA′B′.
如图,点O、B的坐标分别为(0,0)(3,0),将△OAB绕O点按逆时针方向旋转90°得到△OA′B′.