题目内容
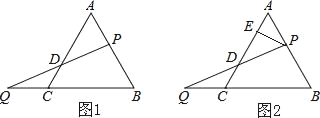
【题目】如图:BD平分∠ABC,∠ABD=∠ADB,∠ABC=50°,请问:
(1)∠BDC+∠C 的度数是多少?并说明理由.
(2)若P点是BC上的一动点(B点除外),∠BDP与∠BPD之和是一个确定的值吗?如果是,求出这个确定的值.如果不是,说明理由.
【答案】(1)∠BDC+∠C=155°,理由见解析,(2)∠BDP与∠BPD之和是一个确定的值,∠BDP+∠BPD=155°,理由见解析.
【解析】
(1)由BD平分∠ABC,∠ABD=∠ADB,可得出AD∥BC,在△BCD中,∠DBC=25°,从而可得答案,
(2)因为∠DBC大小固定,![]() 的大小就固定,所以无论P点如何移动,∠BDP与∠BPD之和为一定值.
的大小就固定,所以无论P点如何移动,∠BDP与∠BPD之和为一定值.
解:(1)∠BDC+∠C=155°. 理由如下:
∵BD平分∠ABC,∠ABC=50°,
∴∠ABD=∠CBD=25°; 又∠ABD=∠ADB=25°,
∠BDC+∠C=180°-∠CBD=155°.
(2)是确定的值. 理由如下:
∵∠ADB=∠CBD,
∴AD∥BC
,∴∠ADP+∠BPD=180°;
∴∠BDP+∠BPD=180°-∠ADB=155°.

【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
【题目】抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
A.当x>1时y随x的增大而增大
B.抛物线的对称轴为x= ![]()
C.当x=2时y=-1
D.方程ax2+bx+c=0一个负数解x1满足-1<x1<0