题目内容
【题目】如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的) 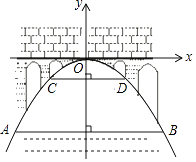
【答案】解:设所求抛物线的解析式为:y=ax2 .
设D(5,b),则B(10,b﹣3),
把D、B的坐标分别代入y=ax2得: ![]() ,
,
解得: 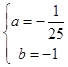 ,
,
∴y=﹣ ![]() x2;
x2;
∵b=﹣1,
∴拱桥顶O到CD的距离为1, ![]() =5小时.
=5小时.
所以再持续5小时到达拱桥顶5小时
【解析】先设抛物线的解析式为y=ax2 , 再找出几个点的坐标,代入解析式后可求得抛物线的解析式,把b=﹣1代入即可求出CD的长度,进而求出时间.

练习册系列答案
相关题目