题目内容
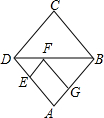 如图菱形ABCD中,EF∥AB,FG∥AD,BF:FD=m:n,CD=15,则EF+FG的长为( )
如图菱形ABCD中,EF∥AB,FG∥AD,BF:FD=m:n,CD=15,则EF+FG的长为( )| A、mn | B、15 | C、6m+9n | D、不能确定,但与m、n的取值有关 |
分析:根据△DEF∽△DAB,△BGF∽△BAD可以求得
+
=1,∵AB=AD=15,∴EF+FG=15.
| EF |
| AB |
| FG |
| AD |
解答:解:∵FG∥AD,EF∥AB,
∴△DEF∽△DAB,△BGF∽△BAD,
∴
=
,
=
,
∵BF+DF=BD,且AB=AD,
∴
+
=
=1,
即EF+FG=AB=CD=15.
故选B.
∴△DEF∽△DAB,△BGF∽△BAD,
∴
| EF |
| AB |
| DF |
| DB |
| FG |
| AD |
| BF |
| BD |
∵BF+DF=BD,且AB=AD,
∴
| EF |
| AB |
| FG |
| AD |
| BD |
| BD |
即EF+FG=AB=CD=15.
故选B.
点评:本题考查了相似三角形对应边的比例相等,考查了菱形四边相等的性质,找到
+
=
=1是解本题的关键.
| EF |
| AB |
| FG |
| AD |
| BD |
| BD |

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
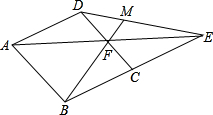 如图菱形ABCD中,∠ABC=120°,F是DC的中点,AF的延长线交BC的延长线于E,则直线BF与直线DE所夹的锐角的度数为( )
如图菱形ABCD中,∠ABC=120°,F是DC的中点,AF的延长线交BC的延长线于E,则直线BF与直线DE所夹的锐角的度数为( )| A、30° | B、40° | C、50° | D、60° |
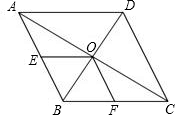
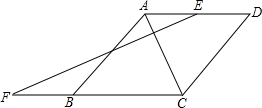 如图菱形ABCD中,点E是AD的中点,EF⊥AC交CB的延长线于点F,交AC于点M,想一想:AB与EF是否互相平分,并说明理由.
如图菱形ABCD中,点E是AD的中点,EF⊥AC交CB的延长线于点F,交AC于点M,想一想:AB与EF是否互相平分,并说明理由.