题目内容
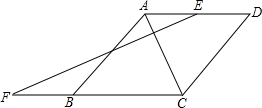
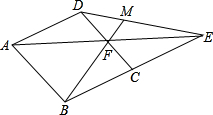如图菱形ABCD中，∠ABC=120°，F是DC的中点，AF的延长线交BC的延长线于E，则直线BF与直线DE所夹的锐角的度数为（ ）| A、30° | B、40° | C、50° | D、60° |
分析：连接BD，可得△BCD是等边三角形，即∠DBM=∠MBC=30°，再由平行线分线段成比例的性质得出CD=CE，即∠CDE=∠CED=30°，进而可求解∠BMD的大小．
解答：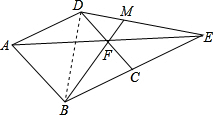
解：连接BD，
则∠BDC=60°，
又∠DCB=60°，BC=CD，
∴△BCD是等边三角形，又F是DC的中点，
∴∠DBM=∠MBC=30°，
∵AD∥BC，∴
=
，
又F是DC的中点，∴AD=CE，
∴CD=CE，又∠ABC=120°，
∴∠CDE=∠CED=30°，
∴∠BMD=∠MBC+∠CED=30°+30°=60°，
故选D．
解：连接BD，则∠BDC=60°，
又∠DCB=60°，BC=CD，
∴△BCD是等边三角形，又F是DC的中点，
∴∠DBM=∠MBC=30°，
∵AD∥BC，∴
| AD |
| CE |
| DF |
| FC |
又F是DC的中点，∴AD=CE，
∴CD=CE，又∠ABC=120°，
∴∠CDE=∠CED=30°，
∴∠BMD=∠MBC+∠CED=30°+30°=60°，
故选D．
点评：本题主要考查了等边三角形的性质以及平行线分线段成比例的性质问题，能够利用其性质求解一些简单的计算问题．
练习册系列答案
相关题目
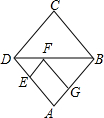如图菱形ABCD中，EF∥AB，FG∥AD，BF：FD=m：n，CD=15，则EF+FG的长为（ ）| A、mn | B、15 | C、6m+9n | D、不能确定，但与m、n的取值有关 |
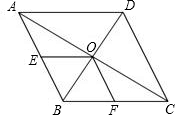
如图菱形ABCD中，点E是AD的中点，EF⊥AC交CB的延长线于点F，交AC于点M，想一想：AB与EF是否互相平分，并说明理由．