题目内容
在如图菱形ABCD中，对角线AC、BD相交于O，E、F分别是AB、BC的中点．求证：OE=OF．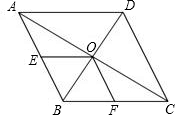
分析：根据菱形的对角线平分且垂直，得△AOB、△BOC为直角三角形，再根据直角三角形中，斜边上的中线等于斜边的一半，从而求得OE=OF．
解答：解：∵AC⊥BD，∴△AOB、△BOC为直角三角形，
∵E、F分别是AB、BC的中点，∴OE=
AB，OF=
BC，
∵AB=BC，∴OE=OF．
∵E、F分别是AB、BC的中点，∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC，∴OE=OF．
点评：本题主要利用菱形的对角线互相垂直平分及直角三角形中，斜边上的中线等于斜边的一半来解决．
练习册系列答案
名校课堂系列答案
相关题目
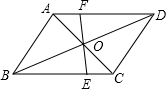如图，?ABCD中，AB⊥AC，AB=1，BC=| 5 |
| A、当∠AOF=90°时，四边形ABEF一定为平行四边形 | ||||
B、当四边形ABEF为直角梯形时，线段EF=
| ||||
| C、当∠AOF=45°时，四边形BEDF一定为菱形 | ||||
| D、在旋转的过程中，线段AF与EC总相等 |
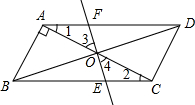如图，?ABCD中，AB⊥AC，AB=1，BC=
