题目内容
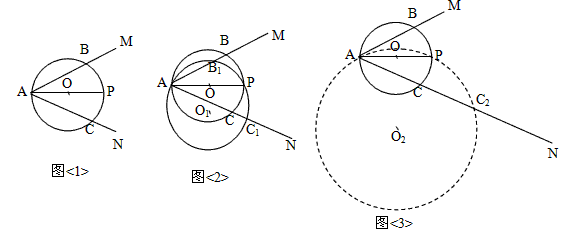
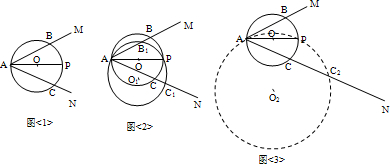
如图,已知:∠MAN=60°,AP平分∠MAN,且AP=4,请探究:
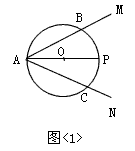
(1)如图<1>,若以AP为直径作⊙O,分别交AM、AN于B、C,求AB+AC的长;
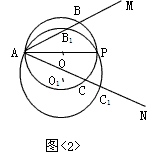
(2)如图<2>,若以AP为弦(不是直径),任作⊙O1分别交AM、AN于B1、C1点,则AB1+AC1的长是否不变?请说明理由;
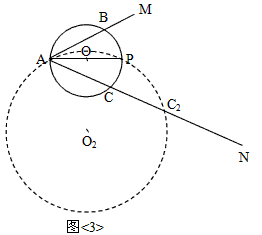
(3)如图<3>,若以AP为弦(不是直径)作⊙O2与AM切于A点,交AN于C2点,则AC2的长是多少?请说明理由。
(1)如图<1>,若以AP为直径作⊙O,分别交AM、AN于B、C,求AB+AC的长;
(2)如图<2>,若以AP为弦(不是直径),任作⊙O1分别交AM、AN于B1、C1点,则AB1+AC1的长是否不变?请说明理由;
(3)如图<3>,若以AP为弦(不是直径)作⊙O2与AM切于A点,交AN于C2点,则AC2的长是多少?请说明理由。
| 解:(1)连接PB、PC, ∵AP为ΘO的直径, ∴∠ABP=∠ACP=90°, ∵AP平分∠MAN, ∴∠BAP=30°, ∴AB=AC=APcos30°= 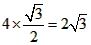 , ,∴AB+AC=4  ; ; |
 |
| (2)AB1+AC1的长度不变, 理由:连接PB1、PC1, 在△PBB1和△PCC1中, ∵∠B1AP=∠C1AP=30°, ∴ 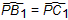 , ,∴PB1=PC1, ∵∠ABP=∠C1CP=90°, ∴PB=PC, ∴Rt△PBB1≌RtPCC1, ∴B1B=C1C, ∴AB1+AC1=AB-B1B+AC+C1C=AB+AC=4  ; ; |
 |
| (3)连接AO2并延长交ΘO2于D,连接PD、PC2, ∴∠APD=90°, 则∠D+∠PAD=90°, ∵ΘO2与AM切于A点, ∴∠PAD+∠BAP=90° =4, ∵∠D=∠BAP=∠CAP=30°, ∵∠D=∠AC2P, ∴∠AC2P=∠CAP, ∴△APC2为等腰三角形, ∵∠ACP=90°,即PC⊥AC2, ∴AC=CC2= 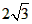 , ,∴AC2=AC+CC2= 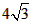 。 。 |
 |

练习册系列答案
相关题目
 如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?
如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?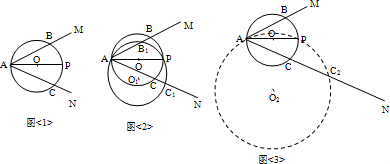
 如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?
如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?