题目内容
【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。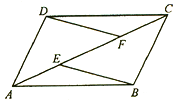
求证:
(1)△ADF≌△CBE
(2)EB∥DF.
【答案】
(1)
证明:∵四边行ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AF=CE.
在△ADF和△CBE中,
|
∴△ADF≌△CBE(SAS).
;
;
;
;
;
;
(2)
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC ,
∴DF∥EB
【解析】(1)由平行四边形的性质得到AD=BC,AD∥BC,和AE=CF去证明;
(2)由(1)△ADF≌△CBE,得到∠DFA=∠BEC , 由内错角相等可知DF∥EB.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目
【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?