题目内容
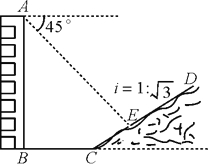
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
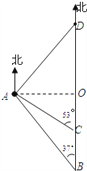
【答案】(1)货船与灯塔A之间的最短距离是36海里,B、C之间的距离是21海里.
(2)A、D之间的距离是60海里.
【解析】试题分析: (1)过点A作AO⊥BC,垂足为O.先解Rt△ACO中,求出CO=ACcos53°≈45×![]() =27,AO=ACsin53°≈45×
=27,AO=ACsin53°≈45×![]() =36.再解Rt△ABO,得到∠OAB=90°-37°=53°,BO=AOtan53°≈36×
=36.再解Rt△ABO,得到∠OAB=90°-37°=53°,BO=AOtan53°≈36×![]() =48,那么BC=BO-CO=48-27=21海里;
=48,那么BC=BO-CO=48-27=21海里;
(2)先根据路程=速度×时间求得BD=48×2=96,那么OD=BD-BO=96-48=48.然后在Rt△AOD中利用勾股定理求出AD=![]() =
=![]() =60海里.
=60海里.
试题解析:
(1)过点A作AO⊥BC,垂足为O.
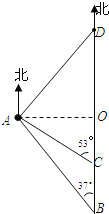
在Rt△ACO中,∵AC=45,∠ACO=53°,
∴CO=ACcos53°≈45×![]() =27,
=27,
AO=ACsin53°≈45×![]() =36.
=36.
在Rt△ABO中,∵AO=36,∠OAB=90°-37°=53°,
∴BO=AOtan53°≈36×![]() =48,
=48,
∴BC=BO-CO=48-27=21,
∴货船与灯塔A之间的最短距离是36海里,B、C之间的距离是21海里.
(2)∵BD=48×2=96,
∴OD=BD-BO=96-48=48.
在Rt△AOD中,∵∠AOD=90°,
∴AD=![]() =
=![]() =60,
=60,
∴A、D之间的距离是60海里.

 阅读快车系列答案
阅读快车系列答案