Question

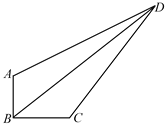
【题目】如图，在四边形ABCD中，∠ABC=90，AB=3，BC=4，CD=10，DA=，则四边形ABCD的面积为=____________，BD的长为____________．

Answer 1

【答案】31；

【解析】

试题解析：连接AC，过点D作DE⊥BC，交BC的延长线与点E．

因为∠ABC=90°，AB=3，BC=4，

∴AC==5，

由于AC2+CD2=25+100=125，AD2=（5）2=125，

∴AC2+CD2=AD2．

所以∠ACD=90°．

所以S四边形ABCD=S△ABD+S△ACD

=ABBC+ACCD

=×3×4+×5×10

=6+25=31．

∵∠DEC=90°，∴∠DCE+∠CDE=90°，

所以∠DCE+∠ACB=90°，

∴∠CDE=∠ACB，又∵∠ABC=90°，

∴△ABC∽△CED

∴CE=6，DE=8．

∴BE=BC+CE=10，

在Rt△DEB中，

DB=.