题目内容
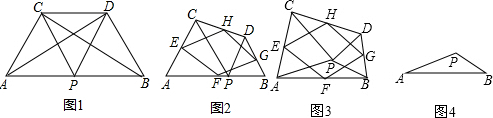
如图1,点O是线段AD的中点,分别以AO,DO为边在AD的同侧作等边△AOB和等边△DOC,AC与BD相交于点E.
(1)根据题意,结合图写出以下结论:
①∠AOC与∠BOD的大小关系是______.
②线段AC与BD的大小关系是______.
③∠AEB=______度.
(2)△OAB固定不动,保持△DOC的形状和大小不变,将△DOC绕着点O旋转,如图2,则(1)中的结论是否仍然成立?试证明你的结论.

(1)解:∵△DCO和△ABO是等边三角形,
∴OC=OD,OB=OA,∠OBA=∠OAB=60°,∠COD=∠BOA=60°,
∴∠COD+∠COB=∠BOA+∠COB,
∴∠DOB=∠COA,
在△DOB和△COA中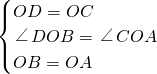 ,
,
∴△DOB≌△COA(SAS),
∴∠AOC=∠BOD,AC=BD,∠DBO=∠CAO,
∵∠OBA=∠OAB=60°
∴∠AEB=180°-(∠EBO+∠OBA+∠BAO)
=180°-(∠CAO+∠OBA+∠BAO)
=180°-(60°+60°)=60°;
故答案分别是:①相等;②相等;③60;
(2)解:(1)中的结论仍然成立.理由如下:与(1)证明过程类似,
∵△DCO和△ABO是等边三角形,
∴OC=OD,OB=OA,∠OBA=∠OAB=60°,∠COD=∠BOA=60°,
∴∠COD+∠COB=∠BOA+∠COB,
∴∠DOB=∠COA,
在△DOB和△COA中 ,
,
∴△DOB≌△COA(SAS),
∴∠DBO=∠CAO,
∵∠OBA=∠OAB=60°
∴∠AEB=180°-(∠EBO+∠OBA+∠BAE)
=180°-(∠CAO+∠OBA+∠BAE)
=180°-(60°+60°)=60°.
分析:(1)通过全等三角形△AOC≌△BOD的对应边相等、对应角相等来求①∠AOC与∠BOD的大小关系、②线段AC与BD的大小关系.在△BEA中,根据三角形内角和定理求出③∠AEB的大小;
(2)求出OC=OD,OA=OB,∠DOB=∠COA,证△DOB≌△COA,推出∠DBO=∠CAO,在△BEA中,根据三角形内角和定理求出即可.
点评:本题考查了等边三角形性质,全等三角形的性质和判定,三角形的内角和定理的应用,关键是求出∠DBO=∠CAO.题目比较好,证明过程类似.
∴OC=OD,OB=OA,∠OBA=∠OAB=60°,∠COD=∠BOA=60°,
∴∠COD+∠COB=∠BOA+∠COB,
∴∠DOB=∠COA,
在△DOB和△COA中
 ,
,∴△DOB≌△COA(SAS),
∴∠AOC=∠BOD,AC=BD,∠DBO=∠CAO,
∵∠OBA=∠OAB=60°
∴∠AEB=180°-(∠EBO+∠OBA+∠BAO)
=180°-(∠CAO+∠OBA+∠BAO)
=180°-(60°+60°)=60°;
故答案分别是:①相等;②相等;③60;
(2)解:(1)中的结论仍然成立.理由如下:与(1)证明过程类似,
∵△DCO和△ABO是等边三角形,
∴OC=OD,OB=OA,∠OBA=∠OAB=60°,∠COD=∠BOA=60°,
∴∠COD+∠COB=∠BOA+∠COB,
∴∠DOB=∠COA,
在△DOB和△COA中
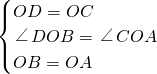 ,
,∴△DOB≌△COA(SAS),
∴∠DBO=∠CAO,
∵∠OBA=∠OAB=60°
∴∠AEB=180°-(∠EBO+∠OBA+∠BAE)
=180°-(∠CAO+∠OBA+∠BAE)
=180°-(60°+60°)=60°.
分析:(1)通过全等三角形△AOC≌△BOD的对应边相等、对应角相等来求①∠AOC与∠BOD的大小关系、②线段AC与BD的大小关系.在△BEA中,根据三角形内角和定理求出③∠AEB的大小;
(2)求出OC=OD,OA=OB,∠DOB=∠COA,证△DOB≌△COA,推出∠DBO=∠CAO,在△BEA中,根据三角形内角和定理求出即可.
点评:本题考查了等边三角形性质,全等三角形的性质和判定,三角形的内角和定理的应用,关键是求出∠DBO=∠CAO.题目比较好,证明过程类似.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目