��Ŀ����
��2012•������һģ����֪���κ�����ͼ��A��2��0����C��0��-12�����㣬�ҶԳ���Ϊֱ��x=4���趥��Ϊ��P����x�����һ����Ϊ��B��
��1������κ����Ľ���ʽ������P�����ꣻ
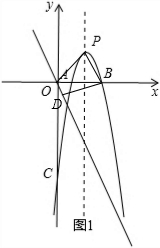
��2����ͼ1����ֱ��y=-2x���Ƿ���ڵ�D��ʹ�ı���OPBDΪ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
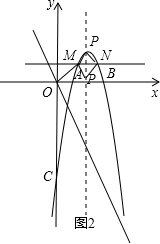
��3����ͼ2����M���߶�OP�ϵ�һ�����㣨O��P������⣩����ÿ��
����λ���ȵ��ٶ��ɵ�P���O�˶�������M��ֱ��MN��x�ᣬ��PB�ڵ�N������PMN��ֱ��MN���ۣ��õ���P1MN���ڶ���M���˶������У����P1MN������OMNB���ص����ֵ����ΪS���˶�ʱ��Ϊt�룮��S�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�

��1������κ����Ľ���ʽ������P�����ꣻ
��2����ͼ1����ֱ��y=-2x���Ƿ���ڵ�D��ʹ�ı���OPBDΪ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2����M���߶�OP�ϵ�һ�����㣨O��P������⣩����ÿ��
| 2 |

��������1������κ����Ľ���ʽΪy=ax2+bx+c������ϵ�������a��b��c��ֵ��������������ߵĽ���ʽ��
��2�����ڵ�D��ʹ�ı���OPBDΪ�������Σ������B������꣬��ֱ��BP�Ľ���ʽΪy=kx+m�������������ֱ�ߵĽ���ʽ����D��x��-2x������BD2=��-2x��2+��6-x��2�����ı���OPBDΪ�������Σ���-2x��2+��6-x��2=32�����x��ֵ��D������꼴�������
��3����0��t��2ʱ����t��ʾ��PH��MH��HN�����ö��κ�����������������亯������ֵ����2��t��4ʱ��P1G=2t-4��P1H=t���������������ƣ����S��P1EF=3t2-12t+12���г�S��t�Ĺ�ϵʽ�����S���ֵ��
��2�����ڵ�D��ʹ�ı���OPBDΪ�������Σ������B������꣬��ֱ��BP�Ľ���ʽΪy=kx+m�������������ֱ�ߵĽ���ʽ����D��x��-2x������BD2=��-2x��2+��6-x��2�����ı���OPBDΪ�������Σ���-2x��2+��6-x��2=32�����x��ֵ��D������꼴�������
��3����0��t��2ʱ����t��ʾ��PH��MH��HN�����ö��κ�����������������亯������ֵ����2��t��4ʱ��P1G=2t-4��P1H=t���������������ƣ����S��P1EF=3t2-12t+12���г�S��t�Ĺ�ϵʽ�����S���ֵ��
��� �⣺��1������κ����Ľ���ʽΪy=ax2+bx+c��
�⣺��1������κ����Ľ���ʽΪy=ax2+bx+c��
�������
��
���
��
�������ߵĽ���ʽΪy=-x2+8x-12����P������Ϊ��4��4����
��2�����ڵ�D��ʹ�ı���OPBDΪ�������Σ��������£�
��y=0ʱ��x2-8x+12=0��
��x1=2��x2=6��
���B��������6��0����
��ֱ��BP�Ľ���ʽΪy=kx+m��
��
��
���
��
��ֱ��BP�Ľ���ʽΪy=-2x+12��
��ֱ��OD��BP��
�߶�������ΪP��4��4����
��OP=4
��
��D��x��-2x������BD2=��-2x��2+��6-x��2��
��BD=OPʱ����-2x��2+��6-x��2=32��
���x1=
��x2=2��
��x2=2ʱ��OD=BP=2
���ı���OPBD��ƽ���ı��Σ���ȥ��
 ��x=
��x=
ʱ�ı���OPBDΪ�������Σ�
�ʵ�D��
��-
��ʱ���ı���OPBDΪ�������Σ�
��3���ٵ�0��t��2ʱ��
���˶��ٶ�Ϊÿ��
�����ȵ�λ���˶�ʱ��Ϊt�룬��MP=
t��
��PH=t��MH=t��HN=
t��
��MN=
t��
��S=
t•t•
=
t2��
��t=2ʱ��S�����ֵ=3��
�ڵ�2��t��4ʱ��P1G=2t-4��P1H=t��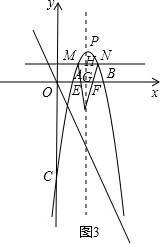
��MN��OB��
���P1EF�ס�P1MN��
��
=��
��2��
��
=��
��2��
��S��P1EF=3t2-12t+12
��S=
t2-��3t2-12t+12��=-
��t-
��2+4��
��t=
ʱ��S�����ֵ=4��
��Ϊ4��3��
��S�������ֵ��S�����ֵΪ4��
 �⣺��1������κ����Ľ���ʽΪy=ax2+bx+c��
�⣺��1������κ����Ľ���ʽΪy=ax2+bx+c���������
|
���
|
�������ߵĽ���ʽΪy=-x2+8x-12����P������Ϊ��4��4����
��2�����ڵ�D��ʹ�ı���OPBDΪ�������Σ��������£�
��y=0ʱ��x2-8x+12=0��
��x1=2��x2=6��
���B��������6��0����
��ֱ��BP�Ľ���ʽΪy=kx+m��
��
|
���
|
��ֱ��BP�Ľ���ʽΪy=-2x+12��
��ֱ��OD��BP��
�߶�������ΪP��4��4����
��OP=4
| 2 |
��D��x��-2x������BD2=��-2x��2+��6-x��2��
��BD=OPʱ����-2x��2+��6-x��2=32��
���x1=
| 2 |
| 5 |
��x2=2ʱ��OD=BP=2
| 5 |
 ��x=
��x=| 2 |
| 5 |
�ʵ�D��
| 2 |
| 5 |
| 4 |
| 5 |
��3���ٵ�0��t��2ʱ��
���˶��ٶ�Ϊÿ��
| 2 |
| 2 |
��PH=t��MH=t��HN=
| 1 |
| 2 |
��MN=
| 3 |
| 2 |
��S=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
��t=2ʱ��S�����ֵ=3��
�ڵ�2��t��4ʱ��P1G=2t-4��P1H=t��

��MN��OB��
���P1EF�ס�P1MN��
��
| S��P1EF |
| S��P1MN |
| P1G |
| P1H |
��
| S��P1EF | ||
|
| 2t-4 |
| t |
��S��P1EF=3t2-12t+12
��S=
| 3 |
| 4 |
| 9 |
| 4 |
| 8 |
| 3 |
��t=
| 8 |
| 3 |
��Ϊ4��3��
��S�������ֵ��S�����ֵΪ4��
������������Ҫ������κ������ۺ����֪ʶ�㣬�����漰��֪ʶ���������߽���ʽ���������߶������꼰�Գ��������������Ҫ���з������ۣ������ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 ��2012•������һģ��һ�����ʾ��ȵ���������������Ϸֱ������ĸA��B��C����չ��ͼ��ͼ��ʾ����������������壬A�泯�ϵĸ�����
��2012•������һģ��һ�����ʾ��ȵ���������������Ϸֱ������ĸA��B��C����չ��ͼ��ͼ��ʾ����������������壬A�泯�ϵĸ�����