题目内容
如图1,点C是线段AB上一动点,分别以线段AC、CB为边,在线段AB的同侧作正方形ACDE和等腰直角三角形BCF,∠BCF=90°,连接AF、BD.
(1)猜想线段AF与线段BD的数量关系和位置关系(不用证明).
(2)当点C在线段AB上方时,其它条件不变,如图2,(1)中的结论是否成立?说明你的理由.
(3)在图1的条件下,探究:当点C在线段AB上运动到什么位置时,直线AF垂直平分线段BD?

(1)猜想线段AF与线段BD的数量关系和位置关系(不用证明).
(2)当点C在线段AB上方时,其它条件不变,如图2,(1)中的结论是否成立?说明你的理由.
(3)在图1的条件下,探究:当点C在线段AB上运动到什么位置时,直线AF垂直平分线段BD?

分析:(1)利用△ACF≌△DCB即可得出AF=BD,进而可得出AF⊥BD;
(2)首先得出△ACF≌△DCB,再利用全等三角形的性质得出AF=BD,以及∠CDB+∠2=90°,进而得出答案;
(3)根据当AC=
AB时,直线AF垂直平分线段BD求出即可.
(2)首先得出△ACF≌△DCB,再利用全等三角形的性质得出AF=BD,以及∠CDB+∠2=90°,进而得出答案;
(3)根据当AC=
| ||
| 2 |
解答: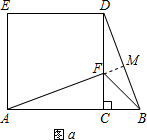 解:(1)如图a,延长AF到DE于点M,
解:(1)如图a,延长AF到DE于点M,
在△ACF和△DCB中,
∵
,
∴△ACF≌△DCB(SAS),
∴AF=BD,∠CAF=∠CDE,
∵∠AFC=∠DFM,∠AFC+∠FAC=90°,
∴∠DFM+∠FDM=90°,
∴AF⊥BD.
(2)答:(1)中的结论仍成立,即AF=BD,AF⊥BD.
理由:如图1,
∵四边形ACDE为正方形,∴∠DCA=90°,AC=CD.
∵∠BCF=90°,CF=BC,∴∠DCA=∠BCF=90°,
∴∠DCA+∠DCF=∠BCF+∠DCF,
即∠ACF=∠DCB,
在△ACF和△DCB中,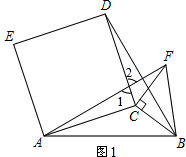
∵
,
∴△ACF≌△DCB(SAS),
∴AF=BD,∠CAF=∠CDB.
又∵∠1=∠2,∠CAF+∠1=90°,∴∠CDB+∠2=90°,
∴AF⊥BD.
(3)探究:当AC=
AB时,直线AF垂直平分线段BD.
如图2,连接AD,则AD=
AC.
∵直线AF垂直平分线段BD,∴AB=AD=
AC,
∴AC=
AB.
 解:(1)如图a,延长AF到DE于点M,
解:(1)如图a,延长AF到DE于点M,在△ACF和△DCB中,
∵
|
∴△ACF≌△DCB(SAS),
∴AF=BD,∠CAF=∠CDE,
∵∠AFC=∠DFM,∠AFC+∠FAC=90°,
∴∠DFM+∠FDM=90°,
∴AF⊥BD.
(2)答:(1)中的结论仍成立,即AF=BD,AF⊥BD.
理由:如图1,
∵四边形ACDE为正方形,∴∠DCA=90°,AC=CD.
∵∠BCF=90°,CF=BC,∴∠DCA=∠BCF=90°,
∴∠DCA+∠DCF=∠BCF+∠DCF,
即∠ACF=∠DCB,
在△ACF和△DCB中,

∵
|
∴△ACF≌△DCB(SAS),
∴AF=BD,∠CAF=∠CDB.
又∵∠1=∠2,∠CAF+∠1=90°,∴∠CDB+∠2=90°,
∴AF⊥BD.
(3)探究:当AC=
| ||
| 2 |

如图2,连接AD,则AD=
| 2 |
∵直线AF垂直平分线段BD,∴AB=AD=
| 2 |
∴AC=
| ||
| 2 |
点评:此题主要考查了正方形的性质以及全等三角判定与性质等知识,熟练利用全等三角形的性质得出对应边与对应角的关系是解题关键.

练习册系列答案
相关题目