题目内容
如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数y=
(k>0)的图象与直线AB相交于C、D两点,若S△OCA=
S△OCD,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).

(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数y=
| k |
| x |
| 1 |
| 8 |
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).

(1)∵A(m,0),B(0,n),
∴OA=m,OB=n.
∴S△AOB=
.
∵m+n=20,
∴n=20-m,
∴S△AOB=
=-
m2+10m=-
(m-10)2+50
∵a=-
<0,
∴抛物线的开口向下,
∴m=10时,S最大=50;
(2)∵m=10,m+n=20,
∴n=10,
∴A(10,0),B(0,10),
设AB的解析式为y=kx+b,由图象,得
,
解得:
,
y=-x+10.
∵S△OCA=
S△OCD,
∴设S△OCD=8a.则S△OAC=a,
∴S△OBD=S△OAC=a,
∴S△AOB=10a,
∴10a=50,
∴a=5,
∴S△OAC=5,
∴
OA•y=5,
∴y=1.
1=-x+10,
x=9
∴C(9,1),
∴1=
,
∴k=9;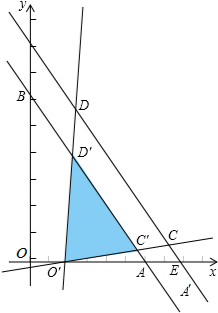
(3)∵C(9,1),
∴D(1,9).
移动后重合的部分的面积是△O′C′D′,t秒后点O的坐标为O′(t,0),
O′A=10-t,O′E=10.
∵C′D′∥CD,
∴△O′C′D′∽△O′CD,
∴
=
=
,
∴
=(
)2=(
)2
S=40•(
)2,
∴S=
t2-8t+40(0<t<10).
∴OA=m,OB=n.
∴S△AOB=
| mn |
| 2 |
∵m+n=20,
∴n=20-m,
∴S△AOB=
| m(20-m) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵a=-
| 1 |
| 2 |
∴抛物线的开口向下,
∴m=10时,S最大=50;
(2)∵m=10,m+n=20,
∴n=10,
∴A(10,0),B(0,10),
设AB的解析式为y=kx+b,由图象,得
|
解得:
|
y=-x+10.
∵S△OCA=
| 1 |
| 8 |
∴设S△OCD=8a.则S△OAC=a,
∴S△OBD=S△OAC=a,
∴S△AOB=10a,
∴10a=50,
∴a=5,
∴S△OAC=5,
∴
| 1 |
| 2 |
∴y=1.
1=-x+10,
x=9
∴C(9,1),
∴1=
| k |
| 9 |
∴k=9;

(3)∵C(9,1),
∴D(1,9).
移动后重合的部分的面积是△O′C′D′,t秒后点O的坐标为O′(t,0),
O′A=10-t,O′E=10.
∵C′D′∥CD,
∴△O′C′D′∽△O′CD,
∴
| O′D′ |
| O′D |
| O′A |
| O′E |
| 10-t |
| 10 |
∴
| S△O′C′D′ |
| S△O′CD |
| O′D′ |
| O′D |
| 10-t |
| 10 |
S=40•(
| 10-t |
| 10 |
∴S=
| 2 |
| 5 |

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目