题目内容
已知抛物线y=ax2+bx+2与x轴相交于点A(x1,0),B(x2,0)(x1<x2),且x1, x2是方程x2-2x-3=0的两个实数根,点C为抛物线与y轴的交点.
x2是方程x2-2x-3=0的两个实数根,点C为抛物线与y轴的交点.(1)求a,b的值;
(2)分别求出直线AC和BC的解析式;
(3)若动直线y=m(0<m<2)与线段AC,BC分别相交于D,E两点,则在x轴上是否存在点P,使得△DEP为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)求出方程两根代入抛物线解析式即可;
(2)设所求的解析式为y=kx+b,用待定系数法求解;
(3)若△DEP为等腰直角三角形,应分情况进行讨论,需注意应符合两个条件:等腰,有直角.
(2)设所求的解析式为y=kx+b,用待定系数法求解;
(3)若△DEP为等腰直角三角形,应分情况进行讨论,需注意应符合两个条件:等腰,有直角.
解答:解:(1)由x2-2x-3=0,得x1=-1,x2=3.
∴A(-1,0),B(3,0),(1分)
把A,B两点的坐标分别代入
y=ax2+bx+2联立求解,
得a=-
,b=
.(2分)
(2)由(1)可得y=-
x2+
x+2,
∵当x=0时,y=2,
∴C(0,2).
设AC:y=kx+b,把A,C两点坐标分别代入y=kx+b,联立求得k=2,b=2.
∴直线AC的解析式为y=2x+2.(3分)
同理可求得直线BC的解析式是y=-
x+2.(4分)
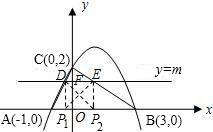 (3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).
①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图,
则△P1DE和△P2ED都是等腰直角三角形,DE=DP1=FO=EP2=m,AB=x2-x1=4.
∵DE∥AB,
∴△CDE∽△CAB,
∴
=
,即
=
.
解得m=
.(6分)
∴点D的纵坐标是
,
∵点D在直线AC上,
∴2x+2=
,解得x=-
,
∴D(-
,
).
∴P1(-
,0),同理可求P2(1,0).(8分)
②当DE为底边时,
过DE的中点G作GP3⊥x轴于点P3,如图,
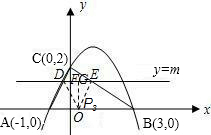
则DG=EG=GP3=m,
由△CDE∽△CAB,
得
=
,即
=
,
解得m=1.(9分)
同1方法.求得D(-
,1),E(
,1),
∴DG=EG=GP3=1
∴OP3=FG=FE-EG=
,
∴P3(
,0).(11分)
结合图形可知,P3D2=P3E2=2,ED2=4,
∴ED2=P3D2+P3E2,
∴△DEP3是Rt△,
∴P3(
,0)也满足条件.
综上所述,满足条件的点P共有3个,即P1(-
,0),P2(1,0),P3(
,0).(12分)
∴A(-1,0),B(3,0),(1分)
把A,B两点的坐标分别代入
y=ax2+bx+2联立求解,
得a=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)由(1)可得y=-
| 2 |
| 3 |
| 4 |
| 3 |
∵当x=0时,y=2,
∴C(0,2).
设AC:y=kx+b,把A,C两点坐标分别代入y=kx+b,联立求得k=2,b=2.
∴直线AC的解析式为y=2x+2.(3分)
同理可求得直线BC的解析式是y=-
| 2 |
| 3 |
 (3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图,
则△P1DE和△P2ED都是等腰直角三角形,DE=DP1=FO=EP2=m,AB=x2-x1=4.
∵DE∥AB,
∴△CDE∽△CAB,
∴
| DE |
| AB |
| CF |
| OC |
| m |
| 4 |
| 2-m |
| 2 |
解得m=
| 4 |
| 3 |
∴点D的纵坐标是
| 4 |
| 3 |
∵点D在直线AC上,
∴2x+2=
| 4 |
| 3 |
| 1 |
| 3 |
∴D(-
| 1 |
| 3 |
| 4 |
| 3 |
∴P1(-
| 1 |
| 3 |
②当DE为底边时,
过DE的中点G作GP3⊥x轴于点P3,如图,

则DG=EG=GP3=m,
由△CDE∽△CAB,
得
| DE |
| AB |
| CF |
| OC |
| 2m |
| 4 |
| 2-m |
| 2 |
解得m=1.(9分)
同1方法.求得D(-
| 1 |
| 2 |
| 3 |
| 2 |
∴DG=EG=GP3=1
∴OP3=FG=FE-EG=
| 1 |
| 2 |
∴P3(
| 1 |
| 2 |
结合图形可知,P3D2=P3E2=2,ED2=4,
∴ED2=P3D2+P3E2,
∴△DEP3是Rt△,
∴P3(
| 1 |
| 2 |
综上所述,满足条件的点P共有3个,即P1(-
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查的知识点较为全面:解一元二次方程,用待定系数法求函数解析式,相似的应用以及勾股定理,等腰三角形的性质等,需耐心分析,加以应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
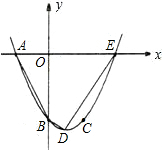 与x轴的另一个交点为E.
与x轴的另一个交点为E.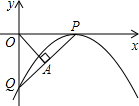 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=