Question

如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-2，0），B（0，-4），C（2，-4）三点，且与x轴的另一个交点为E．
（1）求抛物线的解析式；
（2）用配方法求抛物线的顶点D的坐标和对称轴；
（3）求四边形ABDE的面积．

Answer 1

分析：（1）已知了抛物线上三点的坐标，即可用待定系数法求出抛物线的解析式．
（2）根据（1）的解析式按要求求解即可．
（3）由于四边形ABDE不是规则的四边形，因此可将其分割成几个规则图形来求解．
方法不唯一：①可连接OD，将梯形的面积分割成三个三角形的面积进行求解．
②可过D作x轴的垂线，将梯形的面积分割成两个三角形和一个直角梯形进行求解．

解答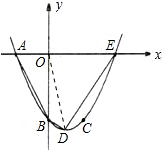：解：（1）∵抛物线y=ax²+bx+c经过A（-2，0），B（0，-4），C（2，-4）三点
∴

4a-2b+c=0 c=-4 4a+2b+c=-4

解得

a= 1 2 b=-1 c=-4

．
∴抛物线解析式：y=

1

2

x²-x-4．

（2）y=

1

2

x²-x-4=

1

2

（x-1）²-

9

2

∴顶点坐标D（1，-

9

2

），对称轴直线x=1．

（3）连接OD，对于抛物线解析式y=

1

2

x²-x-4
当y=0时，得x²-2x-8=0，
解得：x₁=-2，x₂=4．
∴E（4，0），OE=4．
∴S_{四边形ABDE}=S_△AOB+S_△BOD+S_△EOD=

1

2

OA•OB+

1

2

OB•x_{D的横坐标}+

1

2

OEy_{D的纵坐标}=4+2+9=15．

点评：本题主要考查了二次函数解析式的确定以及图形面积的求法等知识点，不规则图形的面积通常转化为规则图形的面积的和差．