题目内容
【题目】如图,在矩形ABCD中,AB=4cm,BC=3cm,点P从点A出发,沿A→B→C向终点C匀速运动,在边AB,BC上分别以4cm/s,3cm/s的速度运动,同时点Q从点A出发,沿A→D→C向终点C匀速运动,在边AD,DC上分别以3cm/s,4cm/s的速度运动,连接PQ,设点P的运动时间为t(s),四边形PBDQ的面积为S(cm2).
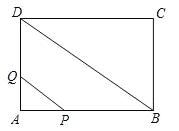
(1)当点P到达边AB的中点时,求PQ的长;
(2)求S与t之间的函数解析式,并写出自变量t的取值范围;
(3)连接DP,当直线DP将矩形ABCD分成面积比为1:5两部分时,直接写出t的值,并写出此时S的值.
【答案】(1)![]() cm;(2)S==-6t2+24t-18(1<t<2);(3)t的值为
cm;(2)S==-6t2+24t-18(1<t<2);(3)t的值为![]() s或
s或![]() s,S=4cm2.
s,S=4cm2.
【解析】
(1)根据题意用t表示出AP、AQ,求出AP,计算即可;
(2)分点P在边AB上、点P在边BC上两种情况,根据矩形面积公式、三角形的面积公式计算;
(3)分点P在边AB上、点P在边BC上两种情况,根据题意列出方程,解方程即可.
解:(1)由题意得,当点P在线段AB上时,AP=4t,AQ=3t,
当点P到达边AB的中点时,AP=2,即4t=2,
解得,t=![]() ,
,
∴AQ=![]() ,
,
∴PQ=![]() (cm);
(cm);
(2)当点P在边AB上时,
S=![]() ×AB×AD-
×AB×AD-![]() ×AP×AQ
×AP×AQ
=6-6t2(0<t<1);
当点P在边BC上时,
CP=3-3(t-1)=6-3t,CQ=4-4(t-1)=8-4t,
S=![]() ×BC×CD-
×BC×CD-![]() ×CP×CQ
×CP×CQ
=-6t2+24t-18(1<t<2);
(3)当点P在边AB上时,由题意得,![]() ×3t×4t=
×3t×4t=![]() ×3×4,
×3×4,
12t2=4,
解得,t=![]() ,
,
当点P在边BC上时,由题意得,![]() ×[3-3(t-1)]×[4-4(t-1)]=
×[3-3(t-1)]×[4-4(t-1)]=![]() ×3×4,
×3×4,
解得,t1=![]() (舍去),t2=
(舍去),t2=![]()
答:当直线DP将矩形ABCD分成面积比为1:5两部分时,t的值为![]() s或
s或![]() s,S=4cm2.
s,S=4cm2.