题目内容
已知菱形ABCD的边长为2,设两邻边AD、AB的夹角为α(α≤90°),图1、图2、图3分别是α为60°,45°,30°时的一组图形,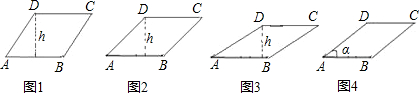
(1)当α=60°时,菱形ABCD的面积为:S=
(2)当α=45°时,菱形ABCD的面积为:S=
(3)当α=30°时,菱形ABCD的面积为:S=
联系与拓展:
(4)如图4,边长为a,两邻边AD、AB的夹角为α(α≤90°)的菱形ABCD的面积为S=
应用:
如图所示,在一个形状为长方形ABCD的广场中,连接各边的中点形成四边形EFGH,此时GH=10m,∠GHE=30°,此部分设计一个图案,若图案铺设每平米需要120元,铺设此图案共需多少元?
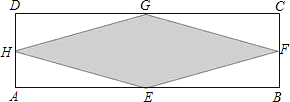
分析:(1)(2)(3)(4)根据三角函数,AB边上的高h=2sinα,再分别代入角α的度数,求得h,根据菱形的面积等于底乘以高求出答案即可;
应用:先判定四边形EFGH为菱形,过点E作EM⊥GF,由直角三角形的性质,求得EM,根据菱形的面积等于底乘以高求出四边形EFGH的面积,再由每平米需要120元得出答案.
应用:先判定四边形EFGH为菱形,过点E作EM⊥GF,由直角三角形的性质,求得EM,根据菱形的面积等于底乘以高求出四边形EFGH的面积,再由每平米需要120元得出答案.
解答:解:(1)∵AD=AB=2,α=60°,∴sinα=
,
∴h=2sinα=2×
=
,
∴S=AB•h=2
;
(2)∵AD=AB=2,α=45°,
∴sinα=
,
∴h=2sinα=2×
=
,
∴S=AB•h=2
;
(3)∵AD=AB=2,α=30°,
∴sinα=
,
∴h=2sinα=2×
=1,
∴S=AB•h=2;
(4)∵AD=AB=2,
∴sinα=
,
∴h=2sinα,
∴S=AB•h=2sinα;
应用:∵四边形ABCD为矩形,E、F、G、H分别为各边的中点,
∴△AEH≌△BEF≌△CGF≌△DGH,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形,
过点E作EM⊥GF,
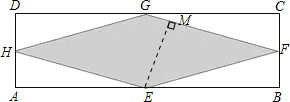
∵GH=10m,∠GHE=30°,
∴EM=5m,
∴S四边形EFGH=GF•EM=GH•EM=10×5=50m2,
∵图案铺设每平米需要120元,
∴铺设此图案共需120×50=6000元.
故答案为:2
; 2
; 2.4sinα.
| h |
| AD |
∴h=2sinα=2×
| ||
| 2 |
| 3 |
∴S=AB•h=2
| 3 |
(2)∵AD=AB=2,α=45°,
∴sinα=
| h |
| AD |
∴h=2sinα=2×
| ||
| 2 |
| 2 |
∴S=AB•h=2
| 2 |
(3)∵AD=AB=2,α=30°,
∴sinα=
| h |
| AD |
∴h=2sinα=2×
| 1 |
| 2 |
∴S=AB•h=2;
(4)∵AD=AB=2,
∴sinα=
| h |
| AD |
∴h=2sinα,
∴S=AB•h=2sinα;
应用:∵四边形ABCD为矩形,E、F、G、H分别为各边的中点,
∴△AEH≌△BEF≌△CGF≌△DGH,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形,
过点E作EM⊥GF,

∵GH=10m,∠GHE=30°,
∴EM=5m,
∴S四边形EFGH=GF•EM=GH•EM=10×5=50m2,
∵图案铺设每平米需要120元,
∴铺设此图案共需120×50=6000元.
故答案为:2
| 3 |
| 2 |
点评:本题考查了菱形的判定和性质,菱形的面积等于底乘以高,要识记.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
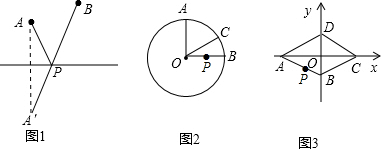
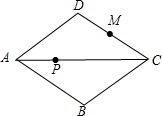 如图,已知菱形ABCD的边长为6,有一内角为60°,M为CD边上的中点,P为对角线AC上的动点,则PD+PM的最小值为
如图,已知菱形ABCD的边长为6,有一内角为60°,M为CD边上的中点,P为对角线AC上的动点,则PD+PM的最小值为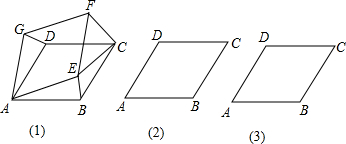 面积.
面积.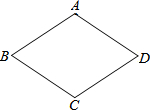 如图,已知菱形ABCD的边AB=2cm,它的周长为
如图,已知菱形ABCD的边AB=2cm,它的周长为