题目内容
“5•12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个粮食基地得知四川C、D两个灾民安置点分别急需粮食120吨和130吨的消息后,决定调运粮食支援灾区.已知A粮食基地有粮食100吨,B粮食基地有粮食150吨,现将这些粮食全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的粮食为x吨.(1)请填写下表,并求两个粮食基地调运粮食的运费相等时x的值;
| C | D | 总计 | |
| A | 100吨 | ||
| B | x吨 | 150吨 | |
| 总计 | 120吨 | 130吨 | 250吨 |
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调运方案.
分析:(1)根据调运方案即可用x表示出从A运往C,D两地的粮食吨数,以及从B运往D地的粮食吨数,进而求出即可;
(2)y与x之间的函数关系式为:y=2x+4600;列不等式方程组解出20≤x≤120,可得y随x的增大而增大.
(3)根据m的取值范围不同,就有不同的调运方案,由0<m<2时,2<m<15时分别得出即可.
(2)y与x之间的函数关系式为:y=2x+4600;列不等式方程组解出20≤x≤120,可得y随x的增大而增大.
(3)根据m的取值范围不同,就有不同的调运方案,由0<m<2时,2<m<15时分别得出即可.
解答:解:(1)填表
依题意得:20(120-x)+25(x-20)=15x+18(150-x).
解得:x=100.
(2)y与x之间的函数关系为:
y=20(120-x)+25(x-20)+15x+18(150-x)=2x+4600.
依题意得
,
∴20≤x≤120,
在y=2x+4600中,
∵2>0,∴y随x的增大而增大,
故当x=20时,总运费最小,
此时调运方案为如下表.
(3)由题意知y=(2-m)x+4600,
∴0<m<2时,(2)中调运方案总运费最小;m=2时,在20≤x≤120的前提下调运方案的总运费不变;
2<m<15时,x=120总运费最小,
其调运方案如下表.
| C | D | 总计 | |
| A | (120-x)吨 | (x-20)吨 | 100吨 |
| B | x吨 | (150-x)吨 | 150吨 |
| 总计 | 120吨 | 130吨 | 250吨 |
解得:x=100.
(2)y与x之间的函数关系为:
y=20(120-x)+25(x-20)+15x+18(150-x)=2x+4600.
依题意得
|
∴20≤x≤120,
在y=2x+4600中,
∵2>0,∴y随x的增大而增大,
故当x=20时,总运费最小,
此时调运方案为如下表.
| C | D | |
| A | 100吨 | 0吨 |
| B | 20吨 | 130吨 |
∴0<m<2时,(2)中调运方案总运费最小;m=2时,在20≤x≤120的前提下调运方案的总运费不变;
2<m<15时,x=120总运费最小,
其调运方案如下表.
| C | D | |
| A | 0吨 | 100吨 |
| B | 120吨 | 30吨 |
点评:此题考查了一次函数的应用以及列方程找等量关系,训练学生列方程解应用题的能力,方案设计问题是初中数学重点题型.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
“5•12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
(2)设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调运方案.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
| C | D | 总计 | |
| A | 200吨 | ||
| B | x吨 | 300吨 | |
| 总计 | 240吨 | 260吨 | 500吨 |
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调运方案.
“5.12”四川汶川8.0级特大地震牵动着亿万国人的心,众志成城,抗震救灾!灾区人民在党和各级政府的领导下,抓住农时投入了灾后的生产.灾区某生产队想安排30个劳动力开垦75亩土地(每个人可参与多种土地的开垦),这些土地可以种蔬菜、水稻和地瓜,如果这些农作物所需的劳动力和预计的产值如下表:
(1)设种蔬菜x亩,水稻y亩,求y与x之间的函数关系式;
(2)请你为生产队长设计一个能使所有土地都种上农作物,全部劳动力都有工作,而且农作物预计总产值达到最高的最佳生产方案;
(3)目前世界粮食紧缺,水稻需求量加大,若水稻预计产值每亩提高10元,其他数据不变,又如何安排生产方案才能达到总产值最高?
| 农作物 劳动力和预计产值 |
蔬菜 | 水稻 | 地瓜 |
| 每亩所需的劳动力(人) | 0.5 | 0.25 | 0.125 |
| 每亩预计的产值 | 100 | 60 | 45 |
(2)请你为生产队长设计一个能使所有土地都种上农作物,全部劳动力都有工作,而且农作物预计总产值达到最高的最佳生产方案;
(3)目前世界粮食紧缺,水稻需求量加大,若水稻预计产值每亩提高10元,其他数据不变,又如何安排生产方案才能达到总产值最高?
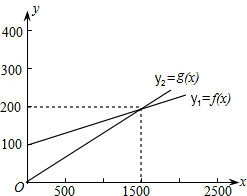 甲出租车公司的月租车费用时y1元,乙车租车公司的月租车费用时y2元,如果y1=f(x),y2=g(x),这两个函数的图象如图所示.
甲出租车公司的月租车费用时y1元,乙车租车公司的月租车费用时y2元,如果y1=f(x),y2=g(x),这两个函数的图象如图所示.