题目内容
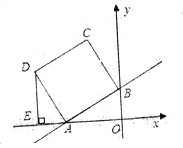
【题目】如图,在平面直角坐标系中,直线y=0.5x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,过点D作DE⊥x轴,垂足为E.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
【答案】(1)、A(-4,0);B(0,2);AB=2![]() ;(2)、(-6,4);(3)、M(-2,0)
;(2)、(-6,4);(3)、M(-2,0)
【解析】
试题分析:(1)、分别令x=0和y=0,求出点B和点A的坐标;(2)、利用△ADE和△AOB全等得出点D的坐标;(3)、作点B关于x轴的对称点F,连接DF与x轴的交点就是点M
试题解析:(1)、当x=0时,y=2;当y=0时,x=-4 ∴A(-4,0) B(0,2)
∴OA=4 OB=2 ∴AB=![]()
(2)、∵ABCD为正方形 ∴AB=AD ∠DAB=90° ∵∠DEA=90°
∴∠EDA+∠DAE=90° ∠DAE+∠BAO=90° ∴∠EDA=∠BAO 又∵∠DEA=∠AOB=90°
∴△ADE≌△BAO ∴DE=A0=4 AE=OB=2 ∴OE=AO+AE=6 ∴点D的坐标为(-6,4)
(3)、作点B关于x轴的对称点F,则点F的坐标为(0,-2)
∴经过点DF的直线解析式为:y=-x-2 当y=0时,x=-2
即点M的坐标为:(-2,0).

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
