题目内容
在平面直角坐标系中,O为坐标原点,已知抛物线 ,点A(2,4).
,点A(2,4).(Ⅰ)求直线OA的解析式;
(Ⅱ)直线x=2与x轴相交于点B,将抛物线C1从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动,设抛物线顶点M的横坐标为m.
①当m为何值时,线段PB最短?
②当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)将抛物线C1作适当的平移,得抛物线
 ,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
,若点D(x1,y1),E(x2,y2)在抛物线C2上,且D、E两点关于坐标原点成中心对称,求c的取值范围.
【答案】分析:(I)直线OA的解析式为y=kx,把点A(2,4)代入即可求出k的值,进而得出直线的解析式;
(II)①由顶点M的横坐标为m,且在线段OA上移动可得出y与m的函数关系式,故可得出抛物线的解析式,当x=2时可得出y与m的函数关系式,进而可得出P点坐标,由m的取值范围即可得出结论;
②当线段PB最短时,抛物线的解析式为y=x2-2x+3,点P的坐标是(2,3).假设在抛物线上存在点Q,使S△QMA=S△PMA,当点Q落在直线OA的下方时,过点P作直线PC∥AO交y轴于点C.PB=3,BA=4,可知直线PC的解析式为y=2x-1,联立直线与抛物线的解析式即可求出Q点的坐标;当点Q落在直线OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,同理可得直线DE的解析式,立直线与抛物线的解析式即可求出Q点的坐标;
(III)由点D、E关于原点成中心对称,可知x2=-x1,y2=-y1,再由D、E两点在抛物线C2上,可得出y与x的关系式,联立直线DE与抛物线的解析式即可得出x2+c=0,点D、E在抛物线C2上,即抛物线C2与直线DE有两个公共点,
解答: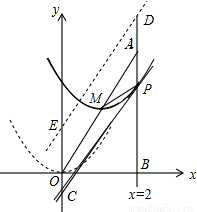 解:(Ⅰ)设直线OA的解析式为y=kx,
解:(Ⅰ)设直线OA的解析式为y=kx,
∵A(2,4),
∴2k=4.
∴k=2.
∴直线OA的解析式为y=2x.
(Ⅱ)①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线的解析式为y=(x-m)2+2m.
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).
∴点P的坐标是(2,m2-2m+4).
∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,线段PB最短.
②当线段PB最短时,抛物线的解析式为y=x2-2x+3,点P的坐标是(2,3).
假设在抛物线上存在点Q,使S△QMA=S△PMA.
当点Q落在直线OA的下方时,过点P作直线PC∥AO交y轴于点C.
∵PB=3,BA=4,
∴AP=1.
∴直线PC的解析式为y=2x-1.
根据题意,列出方程组
∴x2-2x+3=2x-1.
解得x1=2,x2=2.
∴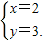 即点Q的坐标是(2,3).
即点Q的坐标是(2,3).
∴点Q与点P重合.
∴此时抛物线上不存在点Q使△QMA与△PMA的面积相等.
当点Q落在直线OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴DA=1.
∴直线DE的解析式为y=2x+1.
根据题意,列出方程组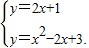
∴x2-2x+3=2x+1.
解得 ,
,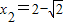 .
.
∴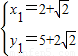 或
或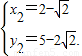
∴此时抛物线上存在点Q1( ,
,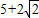 ),Q2(
),Q2(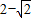 ,
, ),使△QMA与△PMA的面积相等.
),使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点Q1( ,
, ),Q2(
),Q2( ,
,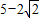 ),使△QMA与△PMA的面积相等.
),使△QMA与△PMA的面积相等.
(Ⅲ)∵点D、E关于原点成中心对称,
∴x2=-x1,y2=-y1①
∵D、E两点在抛物线C2上,
∴ ,②
,②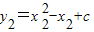 .③
.③
把①代入③,得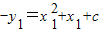 .④
.④
②-④得2y1=-2x1.
∴y1=-x1.
设直线DE的解析式为y=k′x,
由题意,x1≠0,
∴k′=-1.
∴直线DE的解析式为y=-x.
根据题意,列出方程组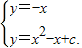
则有x2+c=0,即x2=-c.
∵点D、E在抛物线C2上,即抛物线C2与直线DE有两个公共点,
∴-c>0,即c<0.
∴c的取值范围是c<0.
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、一元二次方程根的判别式等知识,难度较大.
(II)①由顶点M的横坐标为m,且在线段OA上移动可得出y与m的函数关系式,故可得出抛物线的解析式,当x=2时可得出y与m的函数关系式,进而可得出P点坐标,由m的取值范围即可得出结论;
②当线段PB最短时,抛物线的解析式为y=x2-2x+3,点P的坐标是(2,3).假设在抛物线上存在点Q,使S△QMA=S△PMA,当点Q落在直线OA的下方时,过点P作直线PC∥AO交y轴于点C.PB=3,BA=4,可知直线PC的解析式为y=2x-1,联立直线与抛物线的解析式即可求出Q点的坐标;当点Q落在直线OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,同理可得直线DE的解析式,立直线与抛物线的解析式即可求出Q点的坐标;
(III)由点D、E关于原点成中心对称,可知x2=-x1,y2=-y1,再由D、E两点在抛物线C2上,可得出y与x的关系式,联立直线DE与抛物线的解析式即可得出x2+c=0,点D、E在抛物线C2上,即抛物线C2与直线DE有两个公共点,
解答:
 解:(Ⅰ)设直线OA的解析式为y=kx,
解:(Ⅰ)设直线OA的解析式为y=kx,∵A(2,4),
∴2k=4.
∴k=2.
∴直线OA的解析式为y=2x.
(Ⅱ)①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线的解析式为y=(x-m)2+2m.
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).
∴点P的坐标是(2,m2-2m+4).
∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,线段PB最短.
②当线段PB最短时,抛物线的解析式为y=x2-2x+3,点P的坐标是(2,3).
假设在抛物线上存在点Q,使S△QMA=S△PMA.
当点Q落在直线OA的下方时,过点P作直线PC∥AO交y轴于点C.
∵PB=3,BA=4,
∴AP=1.
∴直线PC的解析式为y=2x-1.
根据题意,列出方程组

∴x2-2x+3=2x-1.
解得x1=2,x2=2.
∴
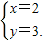 即点Q的坐标是(2,3).
即点Q的坐标是(2,3).∴点Q与点P重合.
∴此时抛物线上不存在点Q使△QMA与△PMA的面积相等.
当点Q落在直线OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴DA=1.
∴直线DE的解析式为y=2x+1.
根据题意,列出方程组
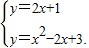
∴x2-2x+3=2x+1.
解得
 ,
,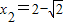 .
.∴
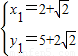 或
或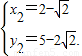
∴此时抛物线上存在点Q1(
 ,
,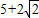 ),Q2(
),Q2(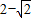 ,
, ),使△QMA与△PMA的面积相等.
),使△QMA与△PMA的面积相等.综上所述,抛物线上存在点Q1(
 ,
, ),Q2(
),Q2( ,
,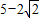 ),使△QMA与△PMA的面积相等.
),使△QMA与△PMA的面积相等. (Ⅲ)∵点D、E关于原点成中心对称,
∴x2=-x1,y2=-y1①
∵D、E两点在抛物线C2上,
∴
 ,②
,②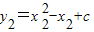 .③
.③把①代入③,得
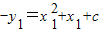 .④
.④②-④得2y1=-2x1.
∴y1=-x1.
设直线DE的解析式为y=k′x,
由题意,x1≠0,
∴k′=-1.
∴直线DE的解析式为y=-x.
根据题意,列出方程组
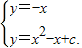
则有x2+c=0,即x2=-c.
∵点D、E在抛物线C2上,即抛物线C2与直线DE有两个公共点,
∴-c>0,即c<0.
∴c的取值范围是c<0.
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、一元二次方程根的判别式等知识,难度较大.

练习册系列答案
相关题目
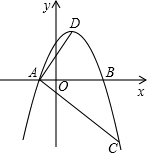 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=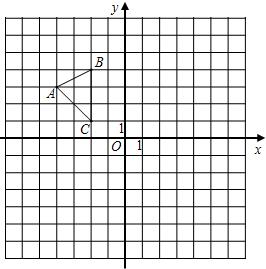 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.