题目内容
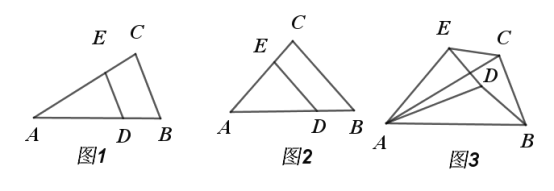
【题目】如图1，在
中，
，点
为
边上的动点，
交
于点
．
问题发现：（1）如图2，当
时，
；
与
所在直线相交所成的锐角等于__________．
类比探究：（2）当
时，把
绕点
逆时针旋转到如图3的位置时，请求出
的值以及与所在直线相交所成的锐角．
【答案】（1）
，45°；（2）
，30°．
【解析】
（1）由
得
，利用相似三角形的性质可得
，然后将AB、AC用EC,BD表示出来,然后再化简并运用锐角的三角函数即可; 
与
所在直线相交所成的锐角等
即可解答．
（2）先说明，再利用相似三角形的性质和
即可说明
∽
，再利用相似三角形的性质和特殊角的三角函数即可求解；
解：（1）∵,
∴,
∴ ，
∴
∴
又∵cos∠=
=cos∠45=
∴
又∵与所在直线相交所成的锐角等于
∴与所在直线相交所成的锐角为45°；
故答案为,45°；
（2）由图1可知，，
∴，
，，
∽，
，
延长交
于点
，交
的延长线于点
，
，
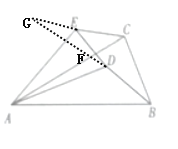
即与所在的直线相交所成的锐角为
，
故答案为：，30°；
练习册系列答案
相关题目
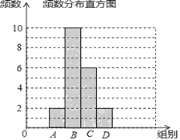
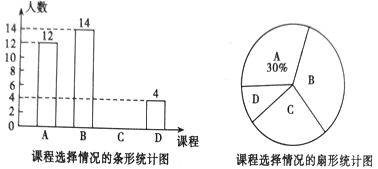
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理，绘制了如下不完整的统计图表：
组别 | 步数分组 | 频率 |
A | x＜6000 | 0.1 |
B | 6000≤x＜7000 | 0.5 |
C | 7000≤x＜8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题：
（1）填空：m＝ ，n＝ ；并补全条形统计图；
（2）这20名朋友一天行走步数的中位数落在 组；（填组别）
（3）张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞，请求出甲、乙被同时点赞的概率．
