Question

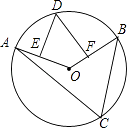
【题目】如图，AB是⊙O的直径，AB=10，∠A=40°，点D为弧BC的中点，点P是直径AB上的一个动点，PC+PD的最小值为 ．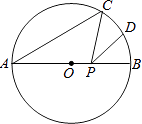

Answer 1

【答案】5
【解析】解：作出D关于AB的对称点D′，连接OC，OD′，CD′．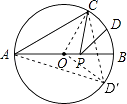

又∵点C在⊙O上，∠CAB=40°，D为 的中点，即 = ，
∴∠BAD′= ∠CAB=20°．
∴∠CAD′=60°．
∴∠COD′=120°，
∵OC=OD′= AB=5，
∴CD′=5 ．
所以答案是：5 ．
【考点精析】本题主要考查了圆周角定理和轴对称-最短路线问题的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径才能正确解答此题．