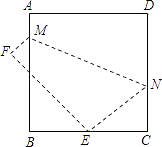
题目内容
【题目】如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD. 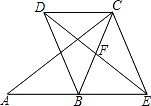
(1)求证:四边形DBEC是平行四边形.
(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中: ①当BE=时,四边形BECD是矩形,试说明理由;
②当BE=时,四边形BECD是菱形.
【答案】
(1)证明:∵AB∥CD,
∴∠CDF=∠FEB,∠DCF=∠EBF,
∵点F是BC的中点,
∴BF=CF,
在△DCF和△EBF中,
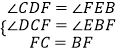 ,
,
∴△EBF≌△DCF(AAS),
∴DC=BE,
∴四边形BECD是平行四边形
(2)2;4
【解析】(2)解:①BE=2; ∵当四边形BECD是矩形时,∠CEB=90°,
∵∠ABC=120°,
∴∠CBE=60°;
∴∠ECB=30°,
∴BE= ![]() BC=2,
BC=2,
所以答案是:2;②BE=4,
∵四边形BECD是菱形时,BE=EC,
∵∠ABC=120°,
∴∠CBE=60°,
∴△CBE是等边三角形,
∴BE=BC=4.
所以答案是:4.
【考点精析】掌握平行四边形的判定和菱形的判定方法是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
相关题目