ƒøƒ⁄»ð
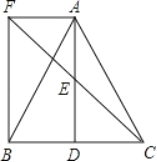
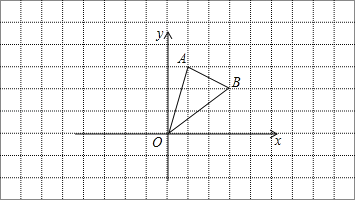
°æƒø°ø»ÁÕº£¨µ»—¸÷±Ω«»˝Ω«–ŒOABµƒ»˝∏ˆ∂®µ„∑÷±Œ™![]() °¢
°¢![]() °¢
°¢![]() £¨π˝A◊˜y÷·µƒ¥πœþ
£¨π˝A◊˜y÷·µƒ¥πœþ![]() .µ„C‘⁄x÷·…œ“‘√ø√Î
.µ„C‘⁄x÷·…œ“‘√ø√Î![]() µƒÀŸ∂»¥”‘≠µ„≥ˆ∑¢œÚ”“‘À∂Ø£¨µ„D‘⁄
µƒÀŸ∂»¥”‘≠µ„≥ˆ∑¢œÚ”“‘À∂Ø£¨µ„D‘⁄![]() …œ“‘√ø√Î
…œ“‘√ø√Î![]() µƒÀŸ∂»Õ¨ ±¥”µ„A≥ˆ∑¢œÚ”“‘À∂Ø£¨µ±Àƒ±þ–ŒABCDŒ™∆Ω––Àƒ±þ–Œ ±C°¢DÕ¨ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™
µƒÀŸ∂»Õ¨ ±¥”µ„A≥ˆ∑¢œÚ”“‘À∂Ø£¨µ±Àƒ±þ–ŒABCDŒ™∆Ω––Àƒ±þ–Œ ±C°¢DÕ¨ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™![]() .µ±C°¢DÕ£÷π‘À∂Ø ±£¨Ω´°˜OAB—ÿy÷·œÚ”“∑≠’€µ√µΩ°˜
.µ±C°¢DÕ£÷π‘À∂Ø ±£¨Ω´°˜OAB—ÿy÷·œÚ”“∑≠’€µ√µΩ°˜![]() £¨
£¨![]() ”ÎCDœýΩª”⁄µ„E£¨PŒ™x÷·…œ¡Ì“ª∂ص„.
”ÎCDœýΩª”⁄µ„E£¨PŒ™x÷·…œ¡Ì“ª∂ص„.
(1)«Û÷±œþABµƒΩ‚Œˆ Ω£¨≤¢«Û≥ˆtµƒ÷µ.
(2)µ±PE+PD»°µ√◊Ó–°÷µ ±£¨«Û![]() µƒ÷µ.
µƒ÷µ.
(3)…ËPµƒ‘À∂ØÀŸ∂»Œ™1£¨»ÙP¥”Bµ„≥ˆ∑¢œÚ”“‘À∂Ø£¨‘À∂Ø ±º‰Œ™![]() £¨«Î”√∫¨
£¨«Î”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ°˜PAEµƒ√ʪ˝.
µƒ¥˙ ˝ Ω±Ì æ°˜PAEµƒ√ʪ˝.

°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª (3)¢Ÿµ±
£ª (3)¢Ÿµ±![]() ±£¨S°˜PAE=
±£¨S°˜PAE=![]() ,¢⁄µ±
,¢⁄µ±![]() ±, S°˜PAE=
±, S°˜PAE=![]() .
.
°æΩ‚Œˆ°ø
£®1£©…Ë÷±œþABŒ™![]() £¨∞—B(-3,0)¥˙»Î£¨«Ûµ√k£¨»∑∂®Ω‚Œˆ Ω£ª‘Ÿ…Ë…Ë
£¨∞—B(-3,0)¥˙»Î£¨«Ûµ√k£¨»∑∂®Ω‚Œˆ Ω£ª‘Ÿ…Ë…Ë![]() √Î∫Ûππ≥…∆Ω––Àƒ±þ–Œ£¨∏˘æð“‚¡–≥ˆ∑Ω≥㨫Û≥ˆtº¥ø…£ª
√Î∫Ûππ≥…∆Ω––Àƒ±þ–Œ£¨∏˘æð“‚¡–≥ˆ∑Ω≥㨫Û≥ˆtº¥ø…£ª
£®2£©π˝E◊˜πÿ”⁄![]() ÷·∂‘”⁄µ„
÷·∂‘”⁄µ„![]() ,¡¨Ω”EE°‰Ωªx÷·”⁄µ„P,‘Ú¥À ±PE+PD◊Ó–°.”…£®1£©µ√µΩµ±t=2 ±£¨”–C£®
,¡¨Ω”EE°‰Ωªx÷·”⁄µ„P,‘Ú¥À ±PE+PD◊Ó–°.”…£®1£©µ√µΩµ±t=2 ±£¨”–C£®![]() £¨0£©£¨D(
£¨0£©£¨D(![]() ,3)£¨‘Ÿ∏˘æðAB°ŒCD£¨«Û≥ˆ÷±œþCD∫ÕAB1µƒΩ‚Œˆ Ω£¨»∑∂®Eµƒ◊¯±Í£ª»ª∫Û‘ŸÕ®π˝≥À∑®π´ Ω∫Õœþ∂Œ‘ÀÀ„£¨º¥ø…ÕÍ≥…Ω‚¥.
,3)£¨‘Ÿ∏˘æðAB°ŒCD£¨«Û≥ˆ÷±œþCD∫ÕAB1µƒΩ‚Œˆ Ω£¨»∑∂®Eµƒ◊¯±Í£ª»ª∫Û‘ŸÕ®π˝≥À∑®π´ Ω∫Õœþ∂Œ‘ÀÀ„£¨º¥ø…ÕÍ≥…Ω‚¥.
£®3£©∏˘æð£®1£©ø…“‘≈–∂œ”–![]() ∫Õ
∫Õ![]() ¡Ω÷÷«Èøˆ£¨»ª∫Û∑÷¿ýÃ÷¬€º¥ø….
¡Ω÷÷«Èøˆ£¨»ª∫Û∑÷¿ýÃ÷¬€º¥ø….
£®1£©Ω‚£∫…Ë÷±œþABŒ™![]() £¨∞—B(-3,0)¥˙»Îµ√£∫
£¨∞—B(-3,0)¥˙»Îµ√£∫
![]()
°ý![]()
°ý![]()
”…“‚µ√£∫
…Ë![]() √Î∫Ûππ≥…∆Ω––Àƒ±þ–Œ£¨‘Ú
√Î∫Ûππ≥…∆Ω––Àƒ±þ–Œ£¨‘Ú
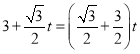
Ω‚÷Ƶ√£∫![]() £¨
£¨
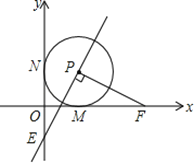
£®2£©»ÁÕº:π˝E◊˜πÿ”⁄![]() ÷·∂‘”⁄µ„
÷·∂‘”⁄µ„![]() ,
,
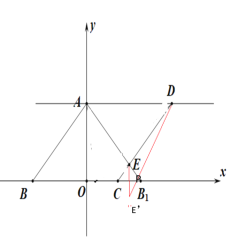
¡¨Ω”EE°‰Ωªx÷·”⁄µ„P,‘Ú¥À ±PE+PD◊Ó–°.
”…£®1£©t=2µ√£∫
°ýC£®![]() £¨0£©£¨D(
£¨0£©£¨D(![]() ,3)
,3)
°þAB°ŒCD
°ý…ËCDŒ™![]()
∞—C£®![]() £¨0£©¥˙»Îµ√
£¨0£©¥˙»Îµ√
b1=![]()
°ýCDŒ™£∫![]()
“◊µ√![]() Œ™£∫
Œ™£∫![]()
°ý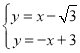
Ω‚÷Ƶ√£∫E(![]() ,
,![]() )
)
°ý
(3)¢Ÿµ±![]() ±
±
S°˜PAE=S°˜PAB1-S°˜PEB1=
![]()
¢⁄µ±![]() ±£∫
±£∫
S°˜PAE=S°˜PAB1-S°˜PEB1=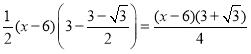

°æƒø°ø»ÁÕº£¨Ω´“ª’≈’˝∑Ω–Œ÷Ω∆¨£¨ºÙ≥…Àƒ∏ˆ¥Û–°–Œ◊¥“ª—˘µƒ–°’˝∑Ω–Œ£¨»ª∫ÛΩ´∆‰÷–µƒ“ª∏ˆ–°’˝∑Ω–Œ‘Ÿ∞¥Õ¨—˘µƒ∑Ω∑®ºÙ≥…Àƒ∏ˆ–°’˝∑Ω–Œ£¨‘ŸΩ´∆‰÷–µƒ“ª∏ˆ–°’˝∑Ω–ŒºÙ≥…Àƒ∏ˆ–°’˝∑Ω–Œ£¨»Á¥À—≠ª∑Ω¯––œ¬»•£ª

£®1£©Ãӱ̣∫
ºÙµƒ¥Œ ˝ | 1 | 2 | 3 | 4 | 5 |
’˝∑Ω–Œ∏ˆ ˝ |
£®2£©»Áπ˚ºÙn¥Œ£¨π≤ºÙ≥ˆ∂ý…Ÿ∏ˆ–°’˝∑Ω–Œ£ø
£®3£©»Áπ˚ºÙ¡À100¥Œ£¨π≤ºÙ≥ˆ∂ý…Ÿ∏ˆ–°’˝∑Ω–Œ£ø
£®4£©π€≤ÏÕº–Œ£¨ºÙ¡Àn¥Œ£¨–°’˝∑Ω–Œµƒ±þ≥§Œ™‘≠¿¥µƒ £¨√ʪ˝ «‘≠¿¥µƒ .