Question

已知一个菱形的周长是20cm，两条对角线的比是4：3，则这个菱形的面积是（　　）

A．12 cm²

B．24 cm²

C．48 cm²

D．96 cm²

Answer 1

分析：由四边形ABCD是菱形，可得OA=

1

2

AC，OB=

1

2

BD，AC⊥BD，又由两条对角线的比是4：3，可设OB=4xcm，OA=3xcm，由勾股定理即可表示出AB的长，又由一个菱形的周长是20cm，即可求得对角线AC与BD的长，继而求得这个菱形的面积．

解答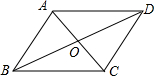：解：如图，∵四边形ABCD是菱形，
∴OA=

1

2

AC，OB=

1

2

BD，AC⊥BD，
∵两条对角线的比是4：3，
∴OB：OA=4：3，
设OB=4xcm，OA=3xcm，
在Rt△AOB中，AB=

OA2+OB2

=5x（cm），
∵一个菱形的周长是20cm，
∴4×5x=20，
解得：x=1，
∴AC=6cm，BD=8cm，
∴这个菱形的面积是：

1

2

AC•BD=

1

2

×6×8=24（cm²）．
故选B．

点评：此题考查了菱形的性质与勾股定理．此题难度不大，注意掌握数形结合思想与方程思想的应用．