��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У���ACBΪ��ǣ���DΪBC����һ���㣬����AD����ADΪֱ�DZ�����AD���Ϸ�������ֱ��������ADF��
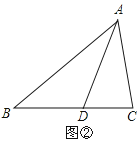
��1����ͼ1����AB=AC����BAC=90�㣬����D���߶�BC��ʱ�������B�غϣ���
֤������ACF�ա�ABD
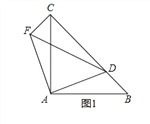
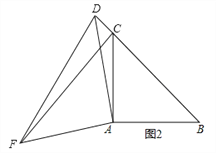
��2����ͼ2������D���߶�BC���ӳ�����ʱ�������������䣬����CF��BD��������ϵ��λ�ù�ϵ��ʲô����˵�����ɣ�
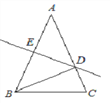
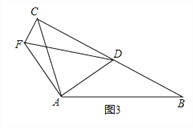
��3����ͼ3����AB��AC����BAC��90�㣬��BCA=45�㣬��D���߶�BC���˶��������B�غϣ�����̽��CF��BDλ�ù�ϵ��
���𰸡�������
����������1������ͬ�ǵ������������CAF=��BAD��Ȼ�����á��߽DZߡ�֤����ACF�͡�ABDȫ�ȣ�
��2���������CAF=��BAD��Ȼ����ٵ�˼·��ͬ��⼴�ɣ�
��3������A��AE��AC��BC��E���ɵá�ACE�ǵ�ֱ�������Σ����ݵ���ֱ�������ε����ʿɵ�AC=AE����AED=45�㣬�ٸ���ͬ�ǵ������������CAF=��EAD��Ȼ�����á��߽DZߡ�֤����ACF�ͼ�AEDȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�ACF=��AED��Ȼ�������BCF=90�㣬�Ӷ��õ�CF��BD.
�⣺��1���ߡ�BAC=90�㣬��ADF�ǵ���ֱ�������Σ�
���CAF+��CAD=90�㣬��BAD+��ACD=90�㣬AD=AF
���CAF=��BAD��������
�ڡ�ACF�͡�ABD�У�
AB=AC����CAF=�ϣ�AD=AF��
���ACF�ա�ABD��SAS��
��2��CF��BD��
��ͼ2���ߡ�ADF�ǵ���ֱ�������Σ�

��AD=AF��
�ߡ�CAB=��DAF=90�㣬
���CAB+��CAD=��DAF+��CAD��
����CAF=��BAD����
�ڡ�ACF�͡�ABD�У�
AB=AC����CAF=��BAD��AD=AF��
���ACF�ա�ABD��SAS������
��CF=BD����ACF=��B��
��AB=AC����BAC=90�㣬���B=��ACB=45�㣬
���BCF=��ACF+��ACB=45��+45��=90�㣬
��CF��BD��
��3��CF��BD
��ͼ3������A��AE��AC��BC��E��

�ߡ�BCA=45�㣬
���ACE�ǵ���ֱ�������Σ�
��AC=AE����AED=45�㣬
�ߡ�CAF+��CAD=90�㣬��EAD+��CAD=90�㣬
���CAF=��EAD������
�ڡ�ACF�͡�AED�У�
AC=AE����CAF=��EAD��AD=AF����
���ACF�ա�AED��SAS��������
���ACF=��AED=45�㣬
���BCF=��ACF+��BCA=45��+45��=90�㣬
��CF��BD��������
���㾦���������������ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ�����ͬ�ǵ�������������ߵļн������֤��������ȫ�ȵĹؼ���������Ŀ���ص��Ǹ�С�����˼·һ�㶼��ͬ.

 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�����Ŀ��(2016����ʡ�����е�21��)ijѧУ����־Ը��Э��Ը��г����Ŀ����������е��飬��ȫ��365���������ȡ��80��Ŀ�������ָ����AQI�����ݣ����Ƴ�������������ͳ��ͼ���������ͼ�����ṩ����Ϣ����������⣺
AQIָ�� | �����ȼ� | �������죩 |
0��50 | �� | m |
51��100 | �� | 44 |
101��150 | �����Ⱦ | n |
151��200 | �ж���Ⱦ | 4 |
201��300 | �ض���Ⱦ | 2 |
300���� | ������Ⱦ | 2 |
��1��ͳ�Ʊ���m= ��n= ������ͳ��ͼ�У����������ȼ�Ϊ������������ռ %��
��2����ȫ����ͳ��ͼ����ͨ��������Ƹ��г���ȫ����������ȼ�Ϊ���������������������������죿
��3���ݵ��飬������Ⱦ��2�췢���ڴ����ڼ䣬ȼ���̻������Ϊ������Ⱦ��һ����Ҫԭ�ݴˣ��������һ�����������飮
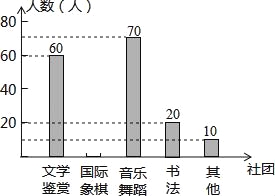
����Ŀ��(2016����ʡ�����е�21��)Ϊ����γ̸ĸijУ������չУ���γ̽��裬�ƻ���������ѧ�����������������������������赸�������鷨���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��������������
ѡ������ | ��ѧ���� | �������� | �����赸 | �鷨 | ���� |
��ռ�ٷֱ� | a | 20% | b | 10% | 5% |
����ͳ��ͼ������Ϣ������������⣺
��1���γ��������ѧ����������a��b��ֵ��
��2��������ͳ��ͼ����������
��3������У����1300��ѧ�����Թ���ȫУѡ���������赸�����ŵ�ѧ��������