题目内容
【题目】如图，A（0，1），M（3，2），N（4，4）.动点P从点A出发，沿轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为t秒.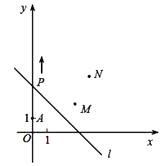
（1）当t＝3时，求l的解析式；
（2）若点M ， N位于l的异侧，确定t的取值范围；
（3）直接写出t为何值时，点M关于l的对称点落在坐标轴上.
【答案】
（1）解:直线 
交y轴于点P（0，b），由题意得 ，b＞0, t≥0 , b=1+t ,
当t=3时，b=4 ∴ 
（2）解:当直线 过M（3,2）时， 
解得b=5
5=1+t
∴t=4
当直线 过N（4,4）时
解得 b=8，8=1+t ∴t=7 ∴ M，N位于l的异侧时，t的取值范围是 ：4<t<7 。
（3）解：如图，过点M作MF⊥直线l，交y轴于点F，交x轴于点E，则点E. F为点M在坐标轴上的对称点。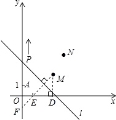
过点M作MD⊥x轴于点D，则OD=3，MD=2.
根据对称性知：∠MED=∠OEF=45，则△MDE与△OEF均为等腰直角三角形，
∴DE=MD=2，OE=OF=1，
∴E(1,0),F(0,1).
∵M(3,2),F(0,1)，
∴线段MF中点坐标为(
,
).
直线y=x+b过点(,),则=+b，解得：b=2，
2=1+t，
解得t=1.
∵M(3,2),E(1,0)，
∴线段ME中点坐标为(2,1).
直线y=x+b过点(2,1)，则1=2+b，解得：b=3，
3=1+t，
解得t=2.
故点M关于l的对称点，当t=1时，落在y轴上，当t=2时，落在x轴上 。
【解析】（1）利用一次函数图象上点的坐标特征，求出一次函数的解析式；
（2）分别求出直线l经过点M、点N时的t值，即可得到t的取值范围；
（3）找出点M关于直线l在坐标轴上的对称点E、F，如解答图所示．求出点E、F的坐标，然后分别求出ME、MF中点坐标，最后分别求出时间t的值．
