题目内容
【题目】(1)如图1,AM∥CN,求证:
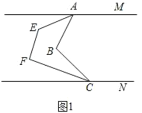

①∠MAB+∠ABC+∠BCN=360°;
②∠MAE+∠AEF+∠EFC+∠FCN=540°;
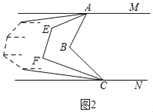
(2)如图2,若平行线AM与CN间有n个点,根据(1)中的结论写出你的猜想并证明.
【答案】(1)①详见解析;②详见解析;(2)猜想:若平行线间有n个点,则所有角的和为(n+1)180°,证明详见解析
【解析】
(1)①过点作BG∥AM,则AM∥CN∥BG,依据平行线的性质,即可得到∠ABG+∠BAM=180°,∠CBG+∠BCN=180°,即可得到结论;②过E作EP∥AM,过F作FQ∥CN,依据平行线的性质,即可得到∠MAE+∠AEP=180°,∠FEP+∠EFQ=180°,∠CFQ+∠FCN=180°,即可得到结论;(2)过n个点作AM的平行线,则这些直线互相平行且与CN平行,即可得出所有角的和为(n+1)180°.
解:(1)①证明:如图1,过点作BG∥AM,则AM∥CN∥BG
∴∠ABG+∠BAM=180°,∠CBG+∠BCN=180°
∴∠ABG+∠BAM+∠CBG+∠BCN=360°
∴∠MAB+∠ABC+∠BCN=360°
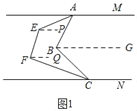
②如图,过E作EP∥AM,过F作FQ∥CN,
∵AM∥CN,∴EP∥FQ,
∴∠MAE+∠AEP=180°,∠FEP+∠EFQ=180°,∠CFQ+∠FCN=180°
∴∠MAE+∠AEF+∠EFC+∠FCN=180°×3=540°;
(2)猜想:若平行线间有n个点,则所有角的和为(n+1)180°.
证明:如图2,过n个点作AM的平行线,则这些直线互相平行且与CN平行,
∴结合(1)问得:
所有角的和为(n+1)180°.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目