题目内容
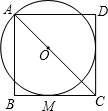 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.
如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.(1)求证:CD与⊙O相切;
(2)若⊙O的半径为1,求正方形ABCD的边长.
分析:(1)过O作ON⊥CD于N,连接OM,由切线的性质可知,OM⊥BC,再由AC是正方形ABCD的对角线可知AC是
∠BCD的平分线,由角平分线的性质可知OM=ON,故CD与⊙O相切;
(2)先根据正方形的性质得出△MOC是等腰直角三角形,由勾股定理可求出OC的长,进而可求出AC的长,在Rt△ABC中,利用勾股定理即可求出AB的长.
∠BCD的平分线,由角平分线的性质可知OM=ON,故CD与⊙O相切;
(2)先根据正方形的性质得出△MOC是等腰直角三角形,由勾股定理可求出OC的长,进而可求出AC的长,在Rt△ABC中,利用勾股定理即可求出AB的长.
解答:(1)证明:过O作ON⊥CD于N,连接OM,
∵⊙O与BC相切于点M,
∴OM⊥BC,
∵四边形ABCD为正方形,
∴∠B=90°,AB∥CD
∴AB∥OM∥DC,
∵AC为正方形ABCD对角线,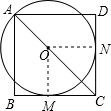
∴∠NOC=∠NCO=∠MOC=∠MCO=45°,
∵OM=ON,
∴CD与⊙O相切;
(2)解:由(1)易知△MOC为等腰直角三角形,OM为半径,
∴OM=MC=1,
∴OC2=OM2+MC2=1+1=2,
∴OC=
.
∴AC=AO+OC=1+
,
在Rt△ABC中,AB=BC,
有AC2=AB2+BC2,
∴2AB2=AC2,
∴AB=
=
.
故正方形ABCD的边长为
.
∵⊙O与BC相切于点M,
∴OM⊥BC,
∵四边形ABCD为正方形,
∴∠B=90°,AB∥CD
∴AB∥OM∥DC,
∵AC为正方形ABCD对角线,

∴∠NOC=∠NCO=∠MOC=∠MCO=45°,
∵OM=ON,
∴CD与⊙O相切;
(2)解:由(1)易知△MOC为等腰直角三角形,OM为半径,
∴OM=MC=1,
∴OC2=OM2+MC2=1+1=2,
∴OC=
| 2 |
∴AC=AO+OC=1+
| 2 |
在Rt△ABC中,AB=BC,
有AC2=AB2+BC2,
∴2AB2=AC2,
∴AB=
1+
| ||
|
| ||
| 2 |
故正方形ABCD的边长为
| ||
| 2 |
点评:本题考查的是正方形的性质及勾股定理、切线的判定与性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.