Question

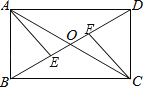
【题目】如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．

（1）求证：AE=CF；

（2）若AB=6，∠COD=60°，求矩形ABCD的面积．

Answer 1

【答案】

【解析】试题分析：（1）由矩形的性质得出OA=OC，OB=OD，AC=BD，∠ABC=90°，证出OE=OF，由SAS证明△AOE≌△COF，即可得出AE=CF；

（2）证出△AOB是等边三角形，得出OA=AB=6，AC=2OA=12，在Rt△ABC中，由勾股定理求出BC的长，即可得出矩形ABCD的面积．

试题解析：（1）证明：∵四边形ABCD是矩形，∴OA=OC，OB=OD，AC=BD，∠ABC=90°，∵BE=DF，∴OE=OF，在△AOE和△COF中，∵OA=OC，∠AOE=∠COF，OE=OF，∴△AOE≌△COF（SAS），∴AE=CF；

（2）解：∵OA=OC，OB=OD，AC=BD，∴OA=OB，∵∠AOB=∠COD=60°，∴△AOB是等边三角形，∴OA=AB=6，∴AC=2OA=12，在Rt△ABC中，BC==，∴矩形ABCD的面积=ABBC=6×=．