题目内容
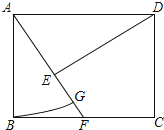
【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

【答案】见解析
【解析】
(1)关键是证出CE=AF,可由AE=AB,AC=BF,两两相加可得.再结合已知条件可证出△AEF≌△CDE .
(2)有(1)中的全等关系,可得出∠AFE=∠CED,再结合△DEF是等边三角形,可知∠DEF=60°,从而得出∠BAC=60°,同理可得∠ACB=60°,那么∠ABC=60°.因而△ABC是等边三角形.
(1)∵BF=AC,AB=AE,
∴BF+AB=AC+AE,即FA=EC.
∵△DEF是等边三角形,∴EF=DE.
又∵AE=CD,∴△AEF≌△CDE.
(2)由△AEF≌△CDE,得∠FEA=∠EDC.
∵△DEF是等边三角形,∴∠DEF=60°.
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
∴∠BCA=60°.同理可得∠BAC=60°,
∴∠ABC=60°,∴△ABC为等边三角形.

【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表 | |||||
项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
人数 | a | 6 | 5 | 7 | 6 |
根据图中提供的信息,解答下列问题: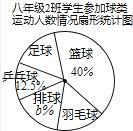
(1)a= , b=
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.