题目内容
已知△ABC中，BC=6cm，E、F分别是AB、AC的中点，那么EF长是分析：利用三角形的中位线定理，知EF是BC的一半，可求出EF．
解答：解：∵△ABC中，E、F分别是AB、AC的中点，
∴EF是△ABC的中位线，
∵BC=6cm，
∴EF=
BC=
×6=3cm．
故答案为3．
∴EF是△ABC的中位线，
∵BC=6cm，
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为3．
点评：本题考查了三角形中位线的性质，本题考查了中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
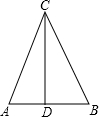如图，已知△ABC中，BC=13cm，AB=10cm，AB边上的中线CD=12cm，则AC的长是（ ）| A、13cm | ||
| B、12cm | ||
| C、10cm | ||
D、
|
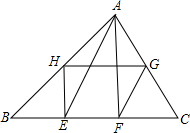如图，已知△ABC中，BC=18，E，F为BC的三等分点，AE=10，AF=8，G，H分别为AC，AB的中点，则四边形EFGH的周长为