题目内容
已知△ABC中，BC＞AC，CH是AB边上的高，且满足| AC2 |
| BC2 |
| AH |
| BH |
分析：由题设条件易想到直角三角形中的基本图形、基本结论，可猜想出∠A与∠B的关系，解题的关键是综合运用勾股定理、比例线段的性质，推导判定两个三角形相似的条件．
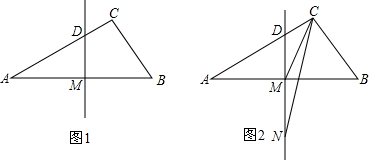
解答：解：（1）若垂线H在线段AB上，如图，
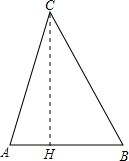
由AH2+CH2=AC2，BH2+CH2=BC2，得，
BH2-AH2=BC2-AC2，
即（BH+AH）（BH-AH）=BC2-AC2
AB=
，由
=
，得
=
，
即
=
，所以AB=
即
=
，
又∠B是△ABC和△CBH的公共角，所以△ABC∽△CHB，
∠ACB=∠CHB=90°，∠A+∠B=90°．
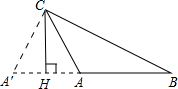
（2）若垂足H在BA的延长线，如图作边CA关于CH的对称线段CA′，
由（1）的结论知：∠A′+∠B=90°，而∠A′=180°-∠A，
代入上式得∠A-∠B=90°．
综上所述（1）（2），知∠A+∠B=90°或∠A-∠B=90°．
由AH2+CH2=AC2，BH2+CH2=BC2，得，
BH2-AH2=BC2-AC2，
即（BH+AH）（BH-AH）=BC2-AC2
AB=
| BC2-AC2 |
| BH-AH |
| AC2 |
| BC2 |
| AH |
| BH |
| BC2-AC2 |
| BC2 |
| BH-AH |
| BH |
即
| BC2-AC2 |
| BH-AH |
| BC2 |
| BH |
| BC2 |
| BH |
| AB |
| BC |
| BC |
| BH |
又∠B是△ABC和△CBH的公共角，所以△ABC∽△CHB，
∠ACB=∠CHB=90°，∠A+∠B=90°．
（2）若垂足H在BA的延长线，如图作边CA关于CH的对称线段CA′，
由（1）的结论知：∠A′+∠B=90°，而∠A′=180°-∠A，
代入上式得∠A-∠B=90°．
综上所述（1）（2），知∠A+∠B=90°或∠A-∠B=90°．
点评：本题考查相似三角形的判定和性质以及三角形的内角和定理，勾股定理等．
练习册系列答案
相关题目
已知△ABC中，BC=6cm，E、F分别是AB、AC的中点，那么EF长是
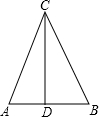如图，已知△ABC中，BC=13cm，AB=10cm，AB边上的中线CD=12cm，则AC的长是（ ）| A、13cm | ||
| B、12cm | ||
| C、10cm | ||
D、
|
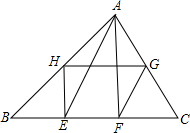如图，已知△ABC中，BC=18，E，F为BC的三等分点，AE=10，AF=8，G，H分别为AC，AB的中点，则四边形EFGH的周长为