题目内容
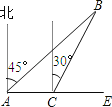
【题目】如图，A，B两点分别位于一个池塘的两端，由于受条件限制无法直接测量A，B间的距离.小明利用学过的知识，设计了如下三种测量方法，如图①、②、③所示（图中a，b，c表示长度）.
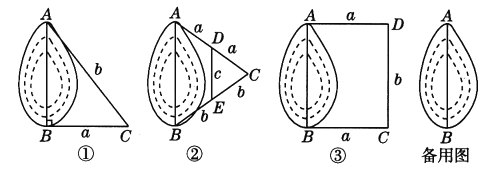
（1）请你写出小明设计的三种测量方法中AB的长度：
图①中，AB=______，图②中，AB=______，图③中，AB=______；
（2）请你再设计一种不同于以上三种的测量方法，画出示意图（不要求写画法）
【答案】（1）①①α
α；②2c；③b; （2）见解析.
【解析】
(1)①结合解直角三角形即可解答,②根据中位线的性质即可填空,③根据矩形的性质即可填空
(2)结合题中所提供的方法及所学知识确定测量方法,并画出草图即可,方法不唯
解：（1）①αα ；②2c；③b.
（2）本题方法很多，下面列出3种供参考.
方法1：如图1.
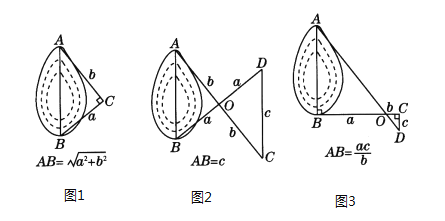
方法2：如图2.
方法3：如图3.
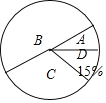
【题目】某市将开展演讲比赛活动，某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计，绘制了如下不完整的统计表和扇形统计图，
成绩等级 | 频数 | 频率 |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
（1）求m、n的值；
（2）求“C等级”所对应的扇形圆心角的度数；
（3）已知成绩等级为A的4名学生中有1名男生和3名女生，现从中随机挑选2名学生代表学校参加全市比赛，求出恰好选中一男生和一女生的概率
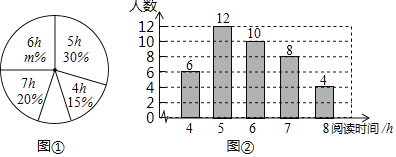
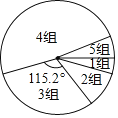
【题目】学习一定要讲究方法，比如有效的预习可大幅提高听课效率．九年级（1）班学习兴趣小组为了了解全校九年级学生的预习情况，对该校九年级学生每天的课前预习时间（单位：
）进行了抽样调查．并将抽查得到的数据分成5组，下面是未完成的频数、顿率分布表和频数分布扇形图．
组别 | 课前预习时间 | 频数（人数） | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
请根据图表中的信息，回答下列问题：
（1）本次调查的样本容量为 ，表中的
，
，
；
（2）试计算第4组人数所对应的扇形圆心角的度数；
（3）该校九年级其有1000名学生，请估计这些学生中每天课前预习时间不少于
的学生人数．