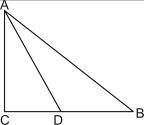
题目内容
如图，在△ABC中，∠ACB＝90°，AC＝5，高CD＝3，则sinA＋sinB等于
A． | B． |
| C．1 | D． |
D
∵∠ACB=90°，
∴∠A+∠B=90°，
又∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠B=∠ACD，
在Rt△ACD中，AC=5，CD=3，
根据勾股定理得：AD=4，
∴在Rt△ACD中，
sinA=
=，sinB=sin∠ACD=
=，
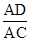则sinA+sinB=+=
故选D
∴∠A+∠B=90°，
又∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠B=∠ACD，
在Rt△ACD中，AC=5，CD=3，
根据勾股定理得：AD=4，
∴在Rt△ACD中，
sinA=
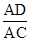=，sinB=sin∠ACD==，则sinA+sinB=
+=故选D
练习册系列答案
相关题目
小时 C．2小时 D．
小时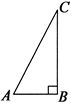
。
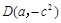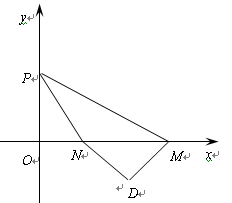
2)若S△MNP＝3S△NOP， ①求sinB的值； ②判断△ABC的三边长能否取一组适当的值，使△
MND是等腰直角三角形？如能，请求出这组值；如不能，请说明理由．
垂足是点E，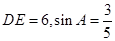
，则菱形ABCD的周长是（ ） 
，迎水坡
，斜坡的坡度角为
，则迎水坡的坡度是____________.
中，
D是BC上的点，
.求AC(
，结果保留整数).